また、底円の面積は $3\times3\times314=26 cm^2$ よって、求める表面積は $おうぎ形の面積底円の面積==\underline{7536cm^2 \dots Ans}$ 計算のコツ 円周率$314$等、 面倒な数値が入る計算は後回し にした方が良い $$ \begin{eqnarray} 表面積 S円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし2 公式を使わない解答 21 おうぎ形の弧の長さを求める;

1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
円錐 表面積 の 求め 方
円錐 表面積 の 求め 方-円錐 体積 表面積 求め方 公式 ツイート 中学1年生では立体を習いますが、立体の体積の求め方の公式は単純なのに対し、表面積の求め方は3通りあります。これらを紹介していくとともに、一つ一つの解法を指導で教える際の注意点を円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!



四角錐 円錐の体積 チーム エン
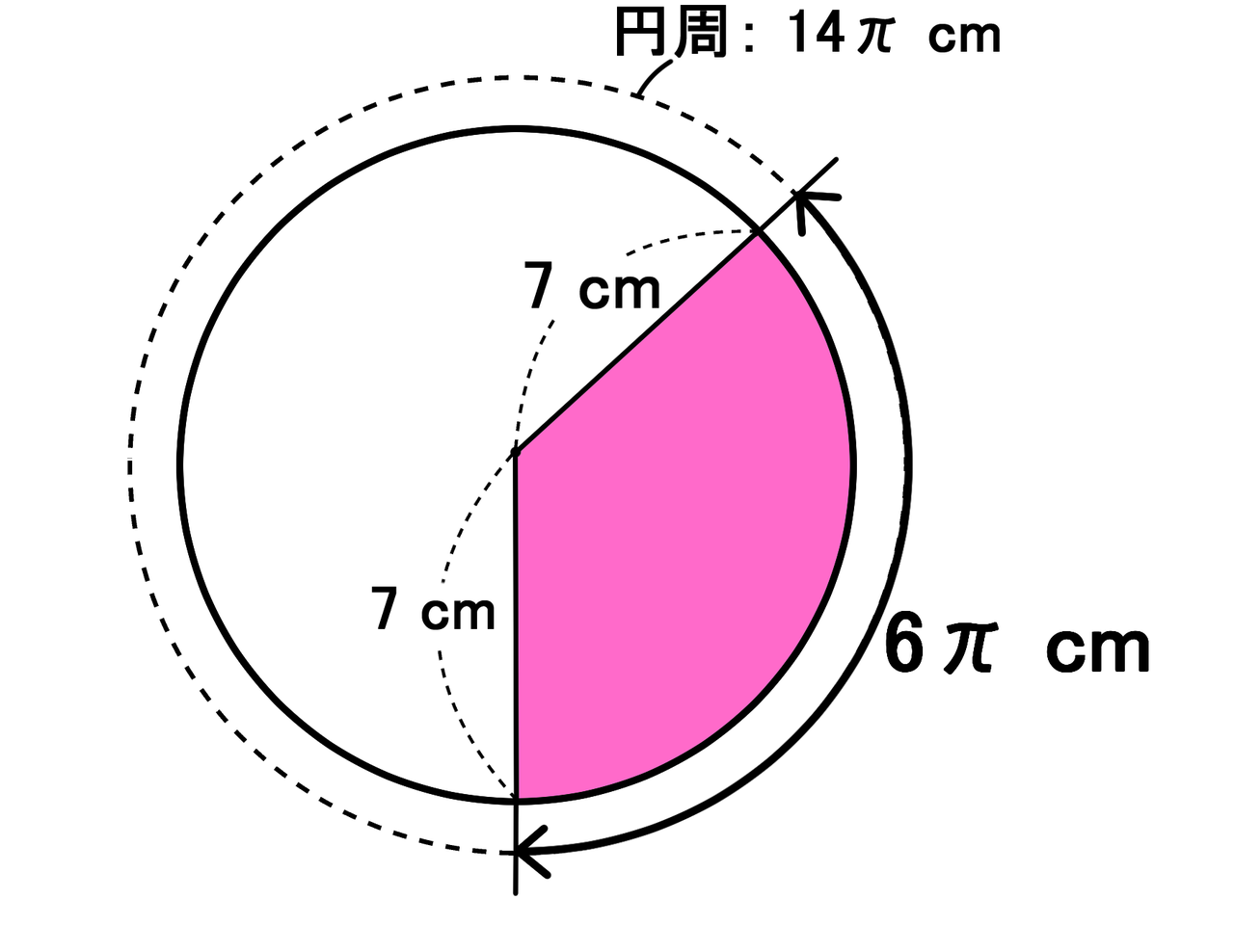
小さな円錐の母線の長さは、三平方の定理を使うと、 $\sqrt{b^2x^2}\\ =\sqrt{b^2\left(\dfrac{bh}{ab}\right)^2}\\ =\dfrac{b}{ab}\sqrt{(ab)^2h^2}$ よって、小さな円錐の側面積は、円錐の側面積の求め方を使うと、 $\pi\times b\times\dfrac{b}{ab}\sqrt{(ab)^2h^2}\\ =\dfrac{\pi b^2}{ab}\sqrt{(ab扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$ こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど!まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。
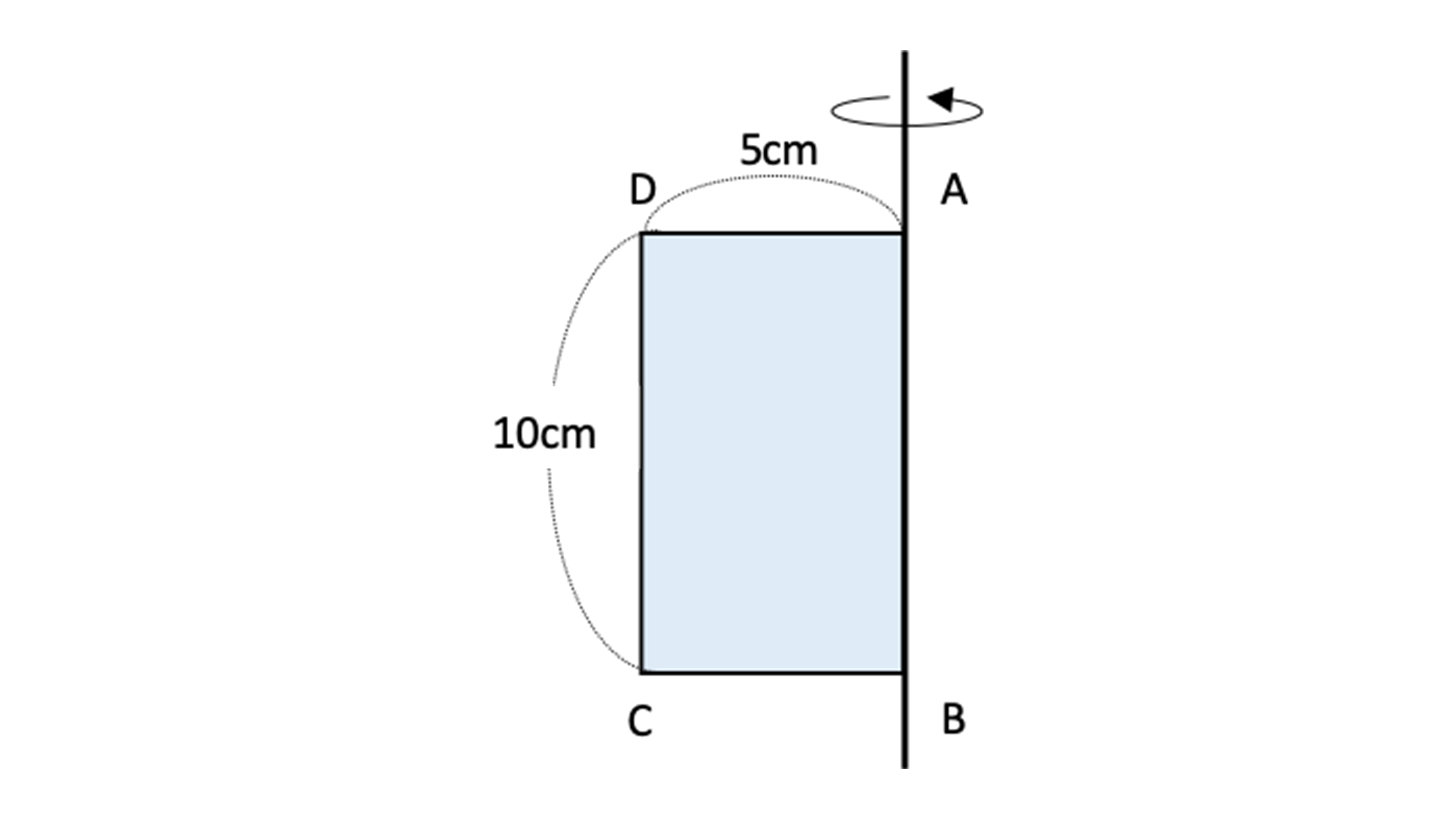
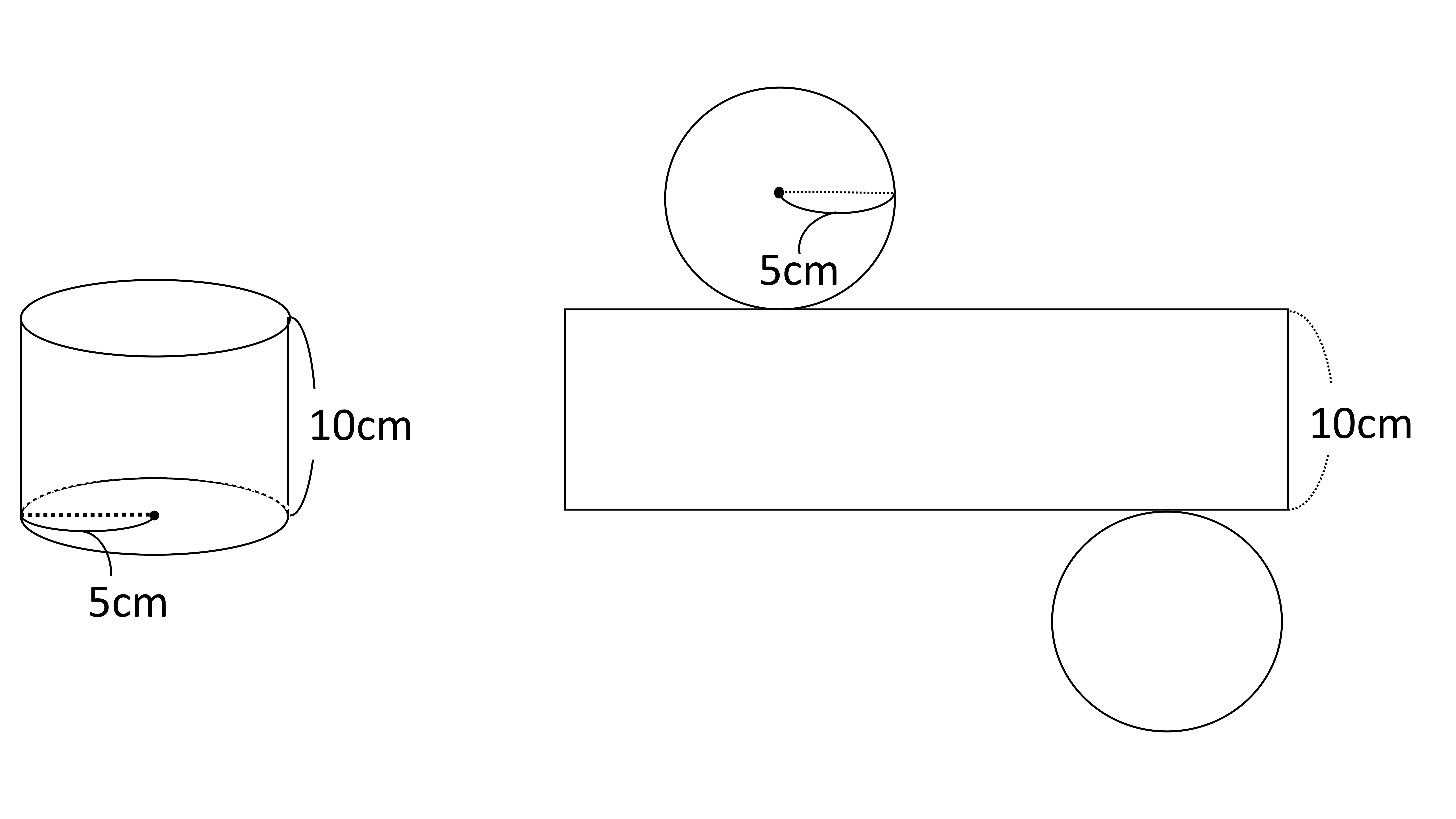
図オの円錐の表面積 この長方形を辺abを軸として1回転させてできる立体の表面積を求めなさい。 は,中学校3年生で習う三平方の定理が必要になります.まだ習っていない場合は,三平方の定理を習ってからやってください.円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!空間図形4回目は表面積の求め方です。いちおう円錐の側面積・表面積の公式も紹介しますが、この連載がめざすのは「応用・難問にであっても解けるような学力」です。よって、円とおうぎ形の基本まで立ち返って解説していきます。 Part 2 Part 2
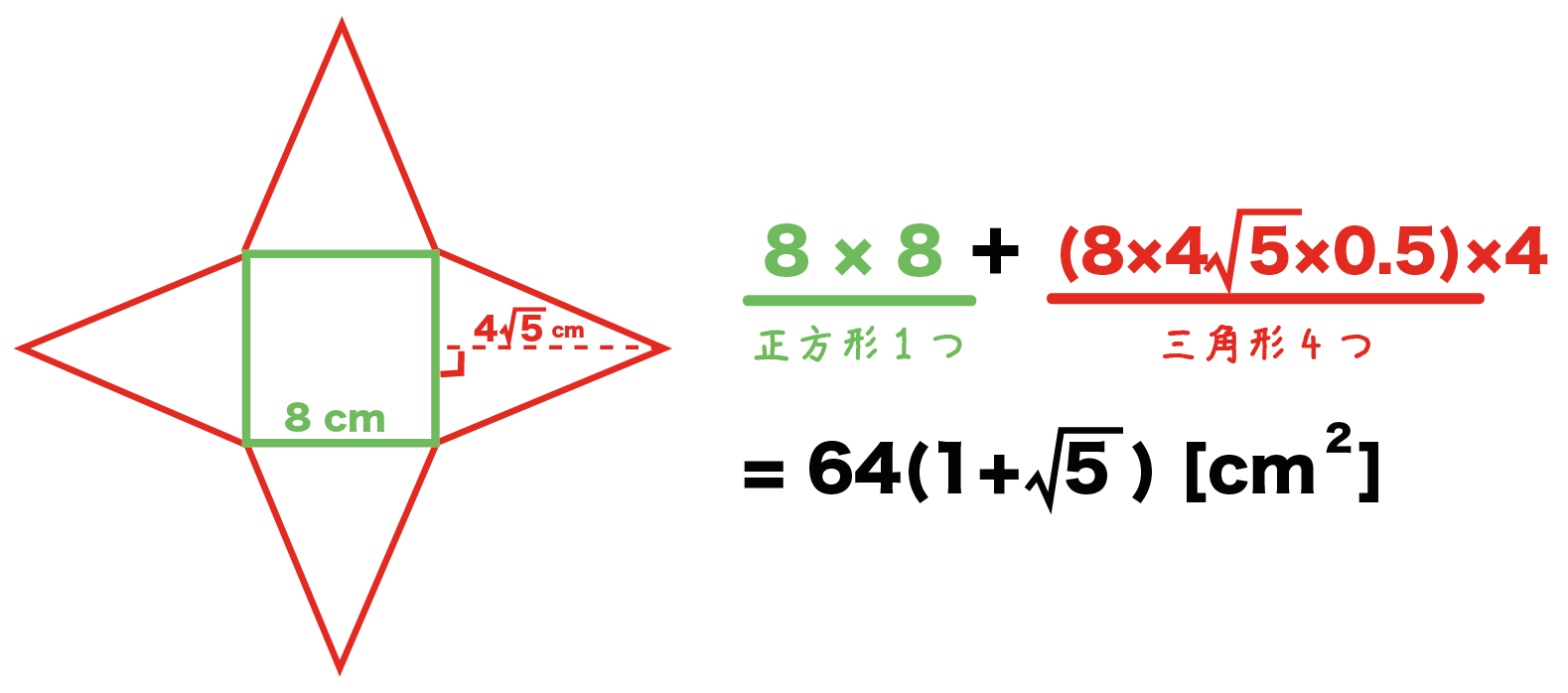
小さな円錐の母線の長さは、三平方の定理を使うと、 $\sqrt{b^2x^2}\\ =\sqrt{b^2\left(\dfrac{bh}{ab}\right)^2}\\ =\dfrac{b}{ab}\sqrt{(ab)^2h^2}$ よって、小さな円錐の側面積は、円錐の側面積の求め方を使うと、 $\pi\times b\times\dfrac{b}{ab}\sqrt{(ab)^2h^2}\\ =\dfrac{\pi b^2}{ab}\sqrt{(ab扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$ こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど!この図形の表面積を求めてください。 どうでしょうか? これは中学1年生の「空間図形」という範囲の 内容です。 なお、 『円錐の表面積の求め方』 で悩んでいる方は ↓こちらをご参照ください↓



最も人気のある 円柱 表面積 公式 壁紙 配布


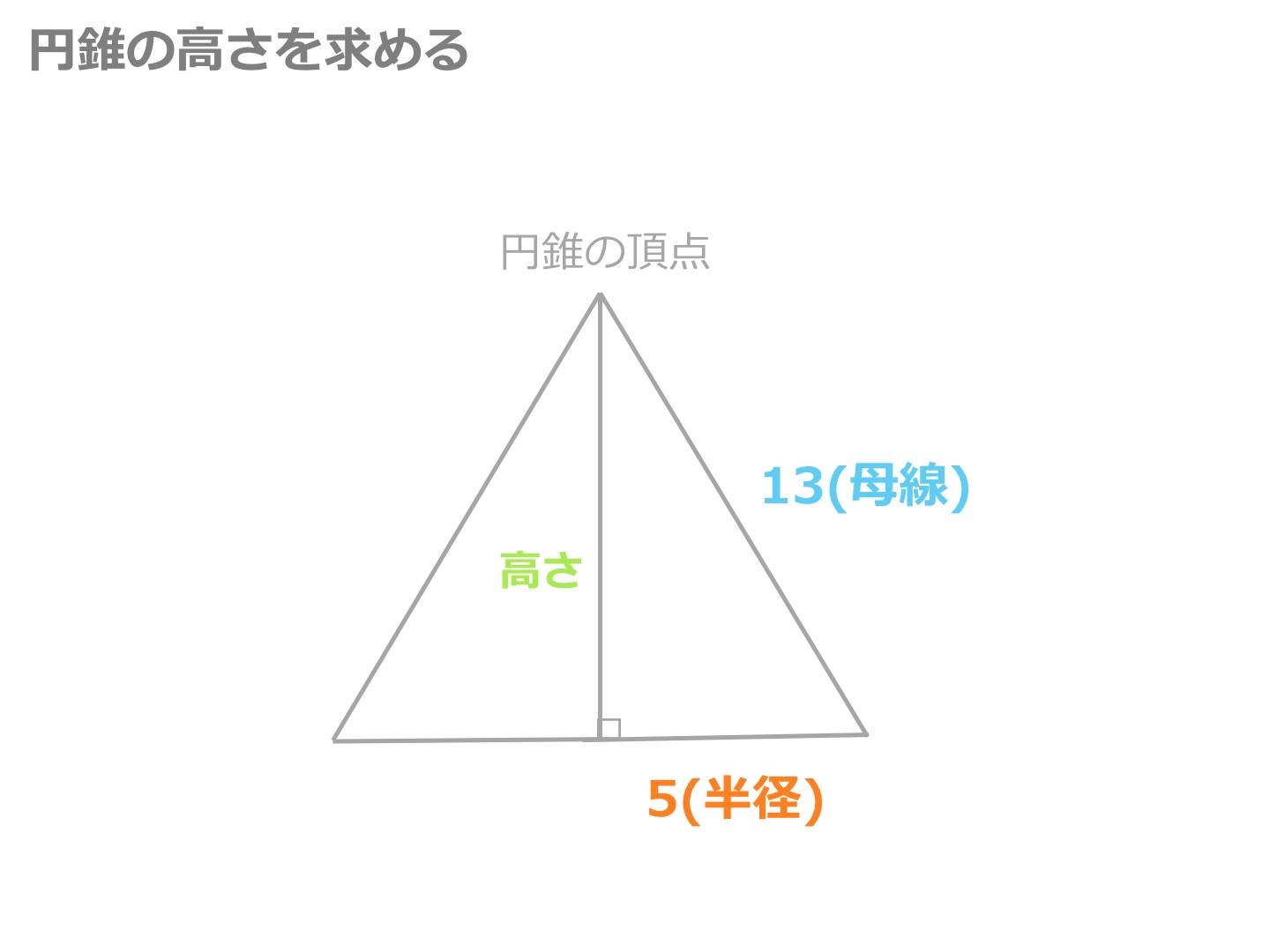
中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐の表面積や体積の求め方すぐ分かる方法を慶応生が解説 Kobun 最高のコレクション 円錐 問題 円錐の表面積や体積の求め方すぐ分かる方法を慶応生が解説 毎日問題を解こう 27 苦手な数学を簡単によって、円柱の表面積は、(側面積)(底面積)より、 $$50\pi90\pi=\underline{140\pi(cm^2)}$$ 映像授業による解説 動画はこちら 3 円すいの表面積を求める問題 問題2 図の円すいの表面積を求めなさい。 問題の見方 手順1 展開図をイメージ円錐の表面積の求め方の公式って?? こんにちは、この記事をかいているKenだよ。梨ジュースはウマいね。 円錐の表面積の求め方の公式 って知ってる?? 円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。 πr(L



中1数学 円錐の表面積のポイント 中学生 数学のノート Clear


1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
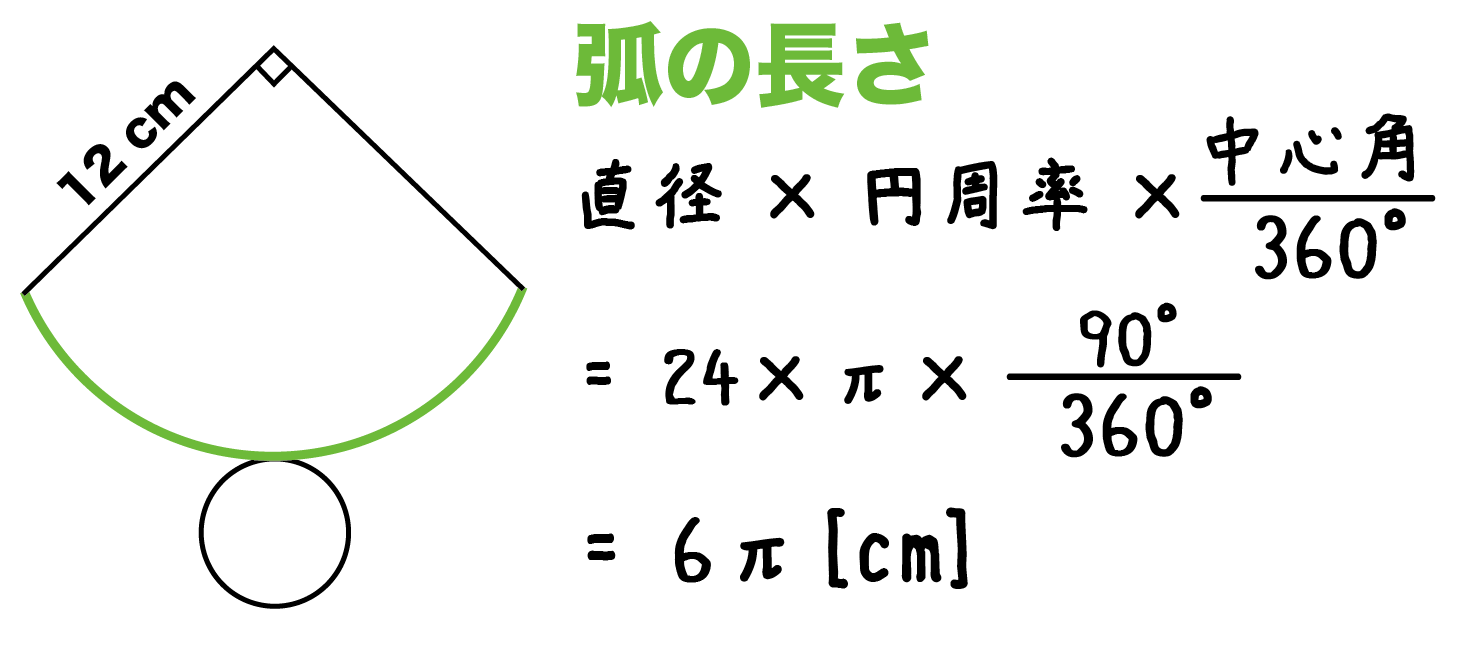
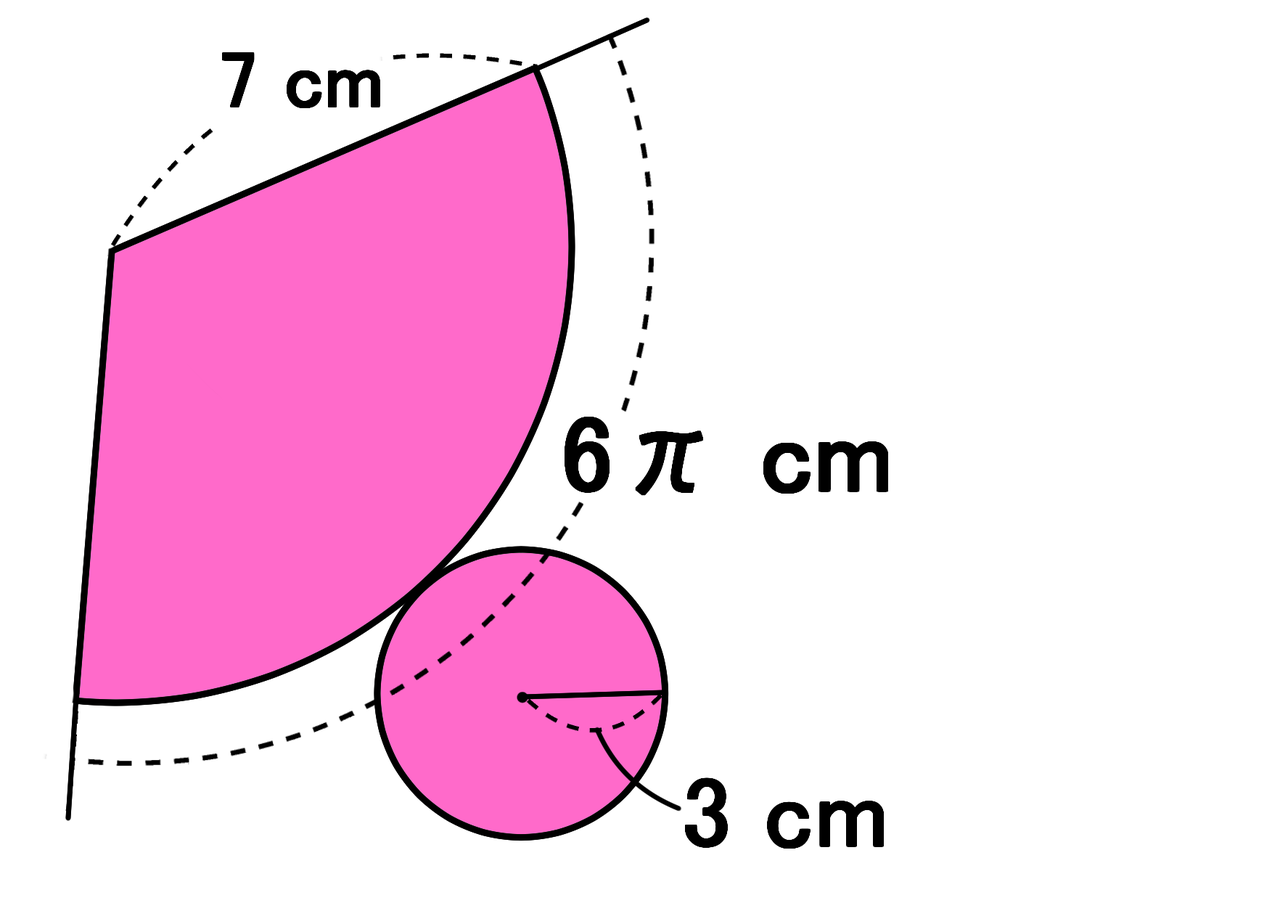
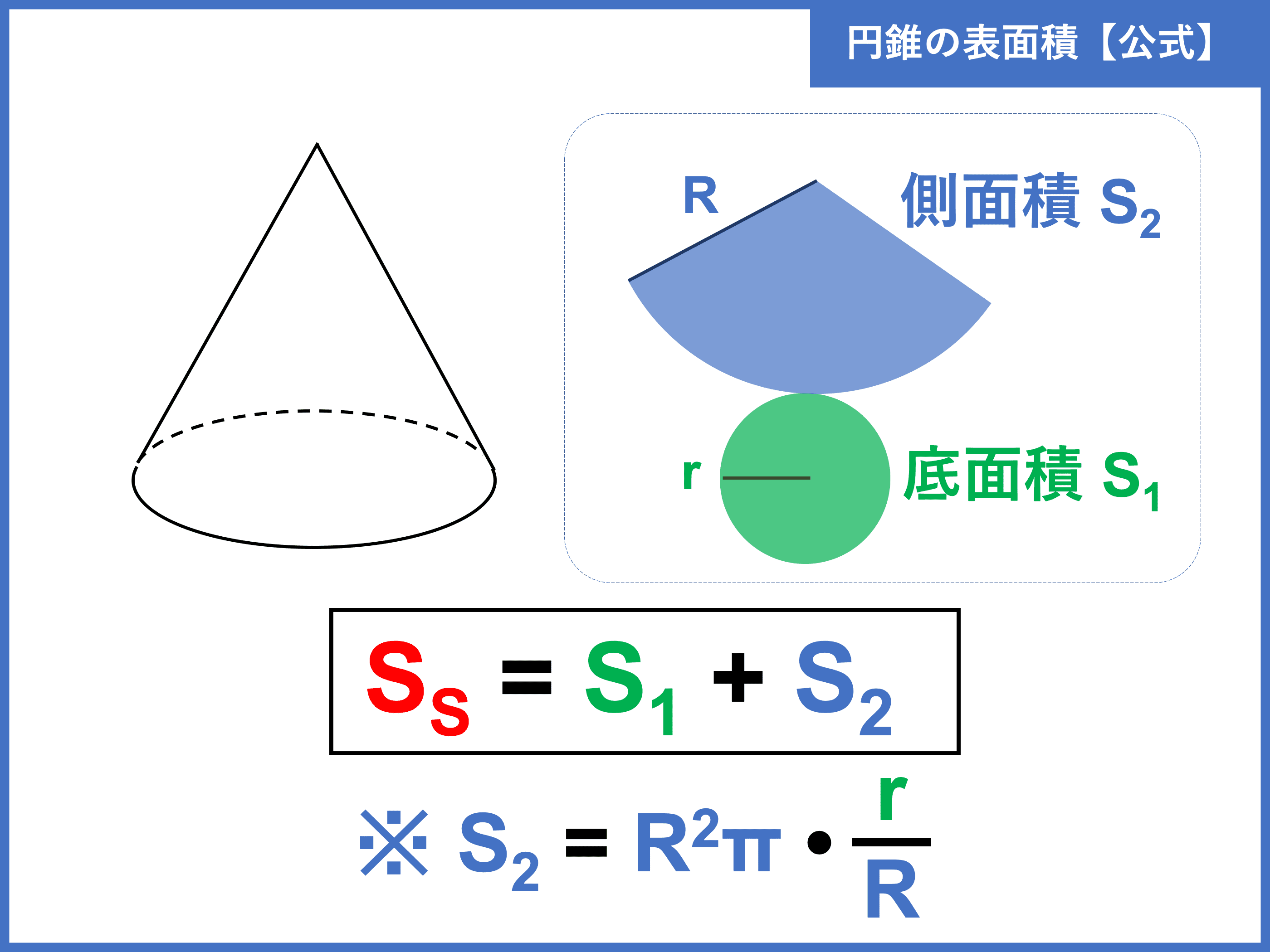
円錐の表面積の求め方 1側面積を求める まずは円錐の側面積を求めていきます。 さて、ここで1つコツを紹介します。 普通に円錐の側面積を求めていこうとするとまずは展開図を書いて、その後中心角を求めて~と長い計算をしていく必要があるわけですが、その手順はめんどくさいですよね?円すいの表面積の求め方の手順とポイントがよくわかりません。 進研ゼミからの回答 次の3つが大きなポイントです。 ・底面(円)と側面(おうぎ形)に分けて求める ・円の円周とおうぎ形の弧の長さが同じ ・おうぎ形空間図形4回目は表面積の求め方です。いちおう円錐の側面積・表面積の公式も紹介しますが、この連載がめざすのは「応用・難問にであっても解けるような学力」です。よって、円とおうぎ形の基本まで立ち返って解説していきます。 Part 2 Part 2



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ
目次 1 公式を使った解答 11 円すいの表面積の公式;円錐や角錐の体積の求め方中学1年数学 柱体や角錐の表面積の求め方中学1年数学 円錐の表面積の求め方中学1年数学 球の表面積や体積の公式と求め方中学1年数学 立体の切断と体積の求め方中学1年数学※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ
3 四角柱の表面積を求める問題 問題2 図の立体は直方体である。この直方体の表面積を求めなさい。 問題の見方 手順1 展開図をイメージ 直方体を展開すると, 底面の2つの四角形 と 側面の長方形 になりますね。 手順2 展開図の面積を求める円錐の表面積を求める公式は、S = πr(rR) で表されます ♦ このページでは、「公式を使う場合」と「使わない場合」に分け、円錐の表面積の求め方を例題と共に説明しています。3 円すい展開図・表面積の公式 の求め方 31 一つの式で書く;



小5 直方体の体積 求め方の工夫 日本語版 Youtube



円錐の表面積を 公式を使って求める チーム エン



四角錐 円錐の体積 チーム エン



โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円柱の表面積 Youtube


1年 円柱の表面積 数学イメージ動画集 大日本図書



表面積の比と体積の比 中学数学に関する質問 勉強質問サイト



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



角錐 円錐の体積 Youtube



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐台 Wikipedia
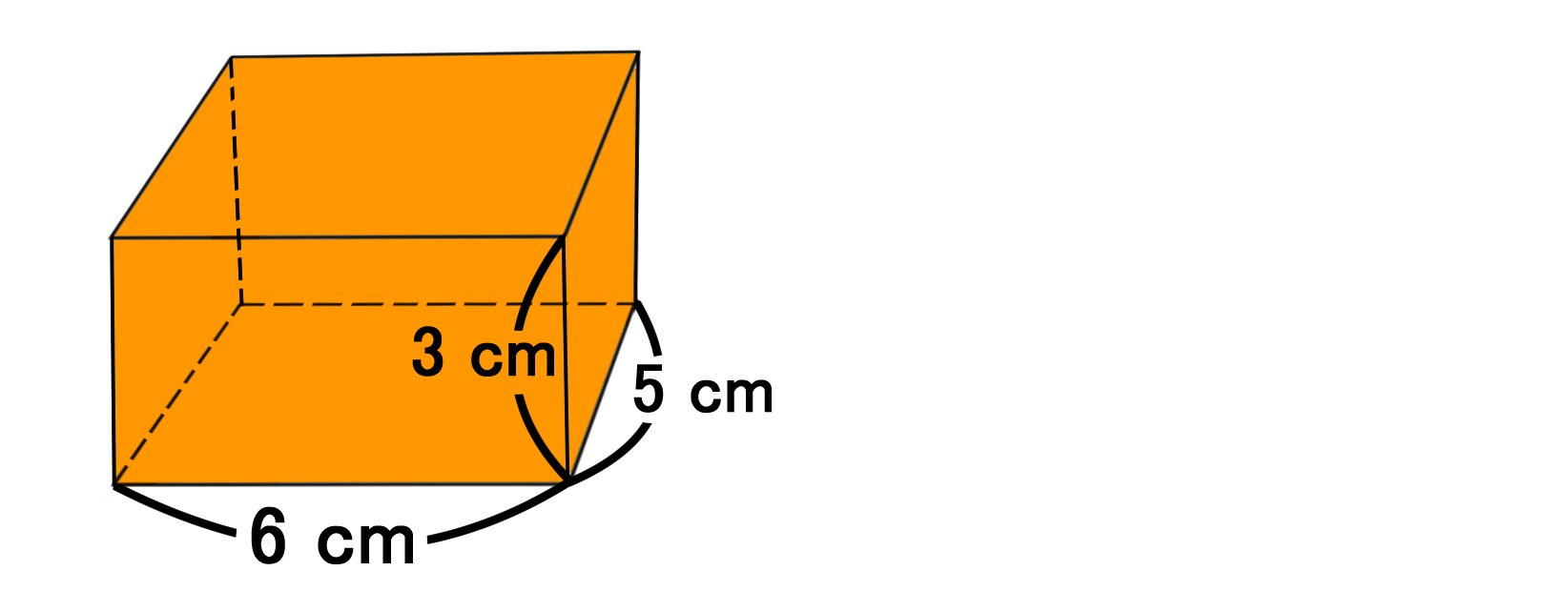


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐の空間図形から表面積を求める基本公式と裏技 現役塾講師のわかりやすい中学数学の解き方



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円錐 展開図 書き方 円錐 作図 ハロウィン かぼちゃ イラスト



中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円周と円周率 面積 表面積 体積の求め方について基本を解説 高校生向け受験応援メディア 受験のミカタ



円錐の体積を求める Youtube



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
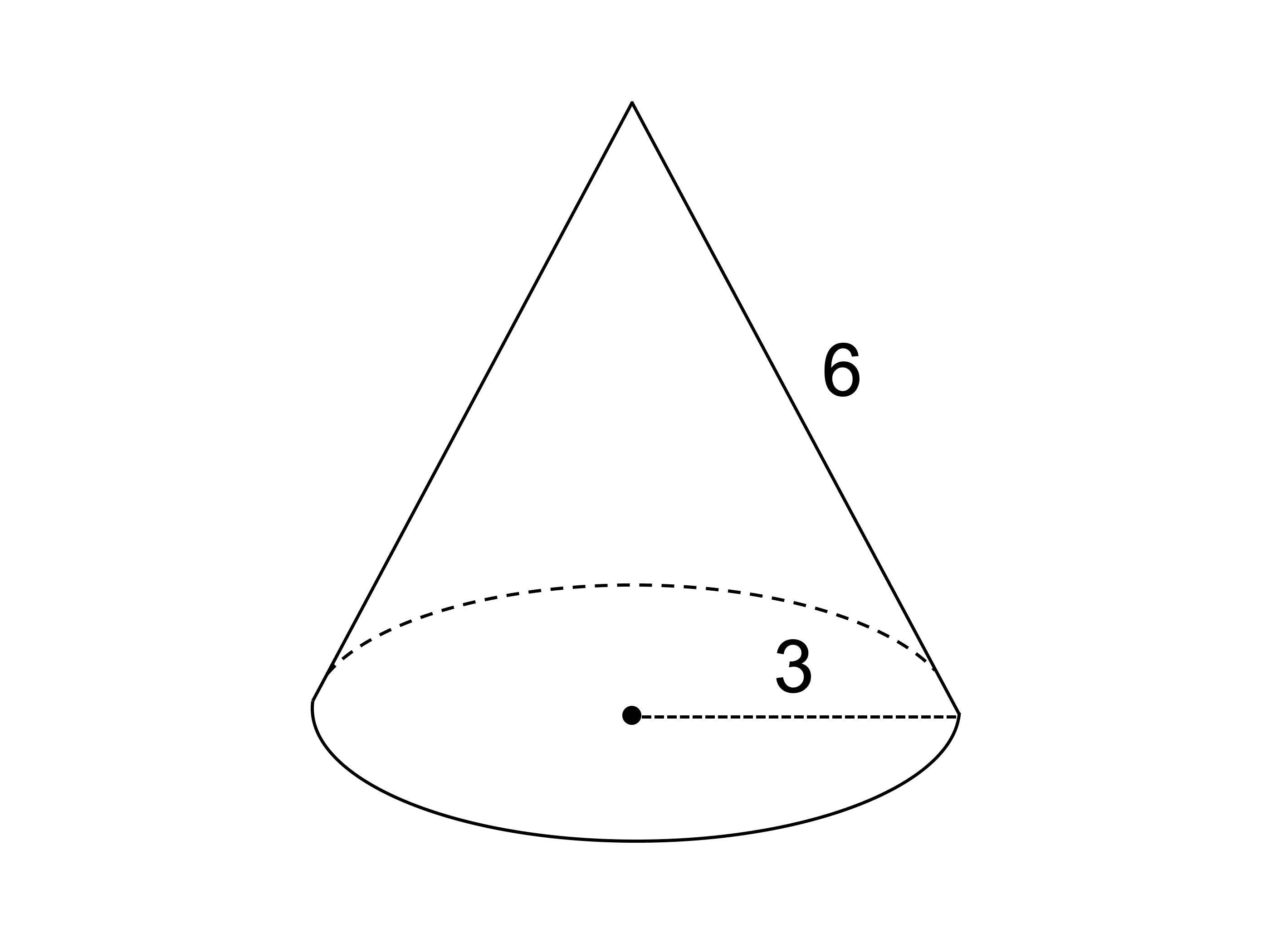


完全版 円錐の展開図の書き方 作り方 受験辞典



簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく 円錐 作図 学び



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



斜軸回転体の体積 応用編 傘型積分 おいしい数学
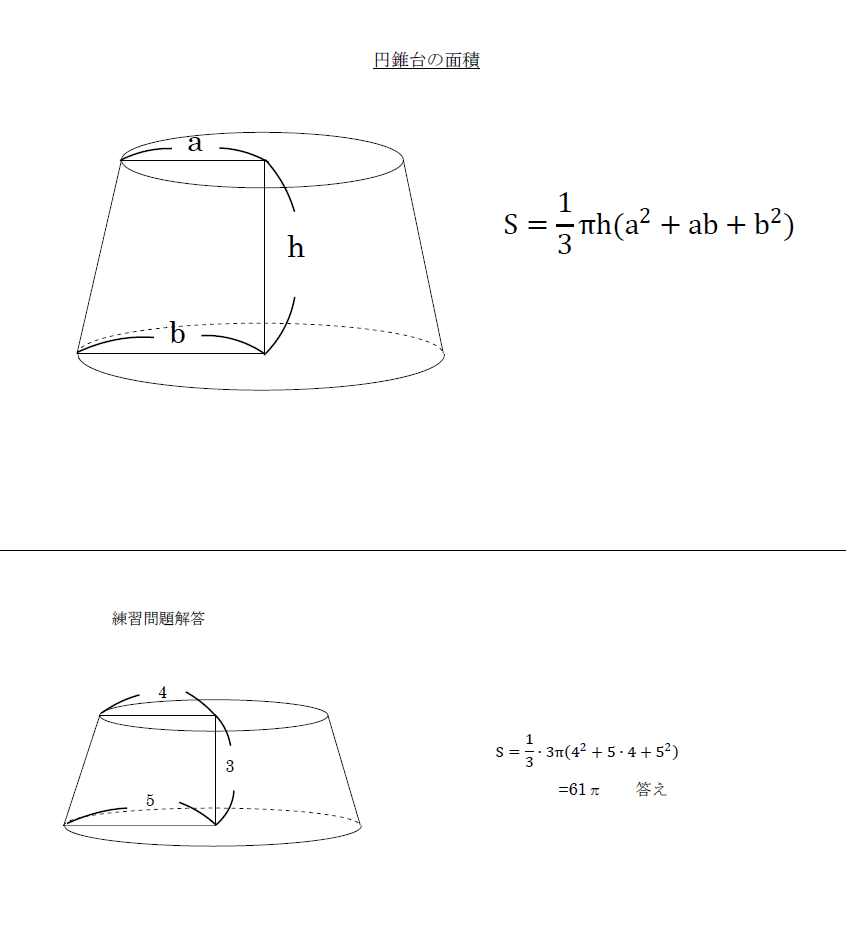


空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
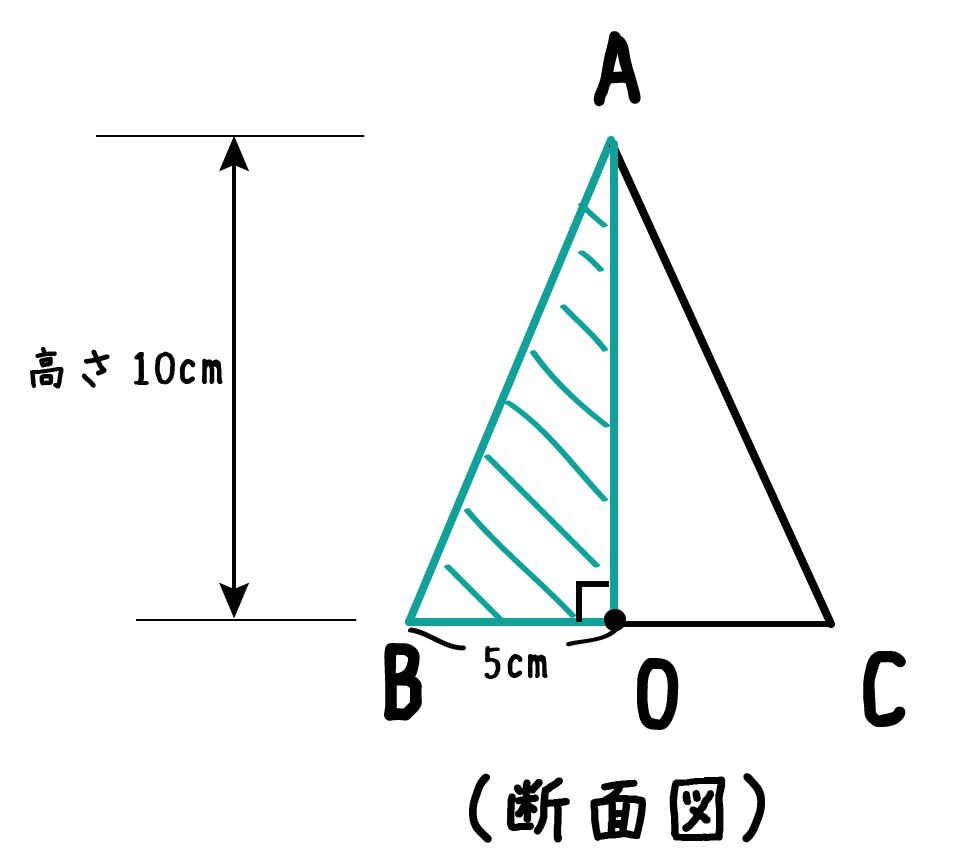


中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく



任意の形をもつ板の円錐への貼付け Autocad Okwave



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく


Tossランド 円錐の表面積 Dl可



円錐と円柱の表面積を簡単に求める方法 Youtube



公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
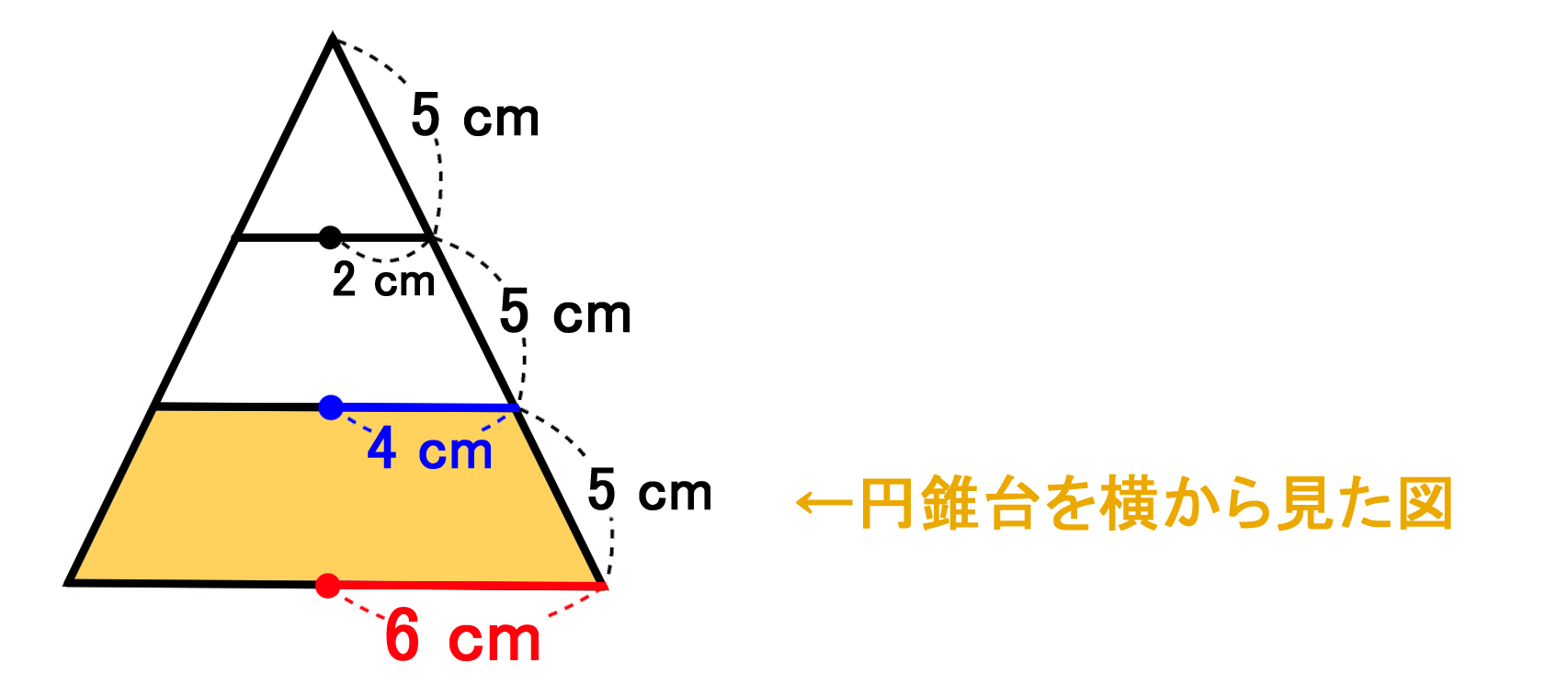


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
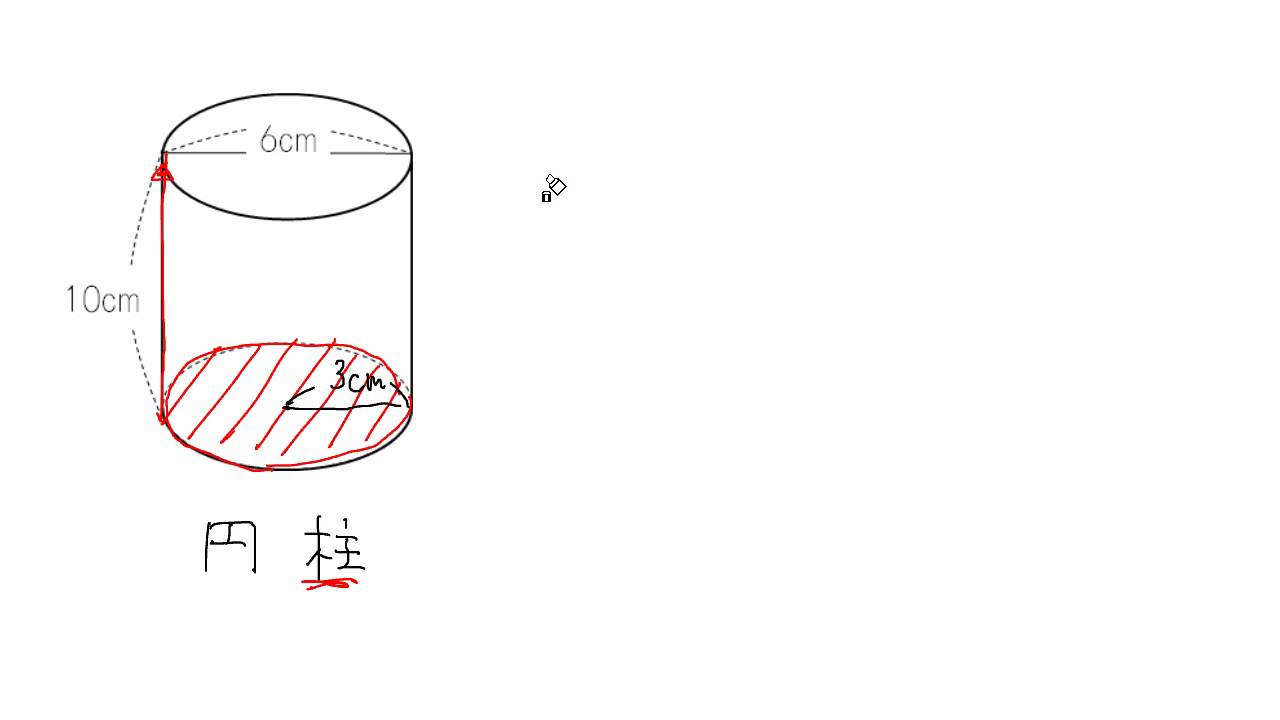


円柱の体積 Youtube
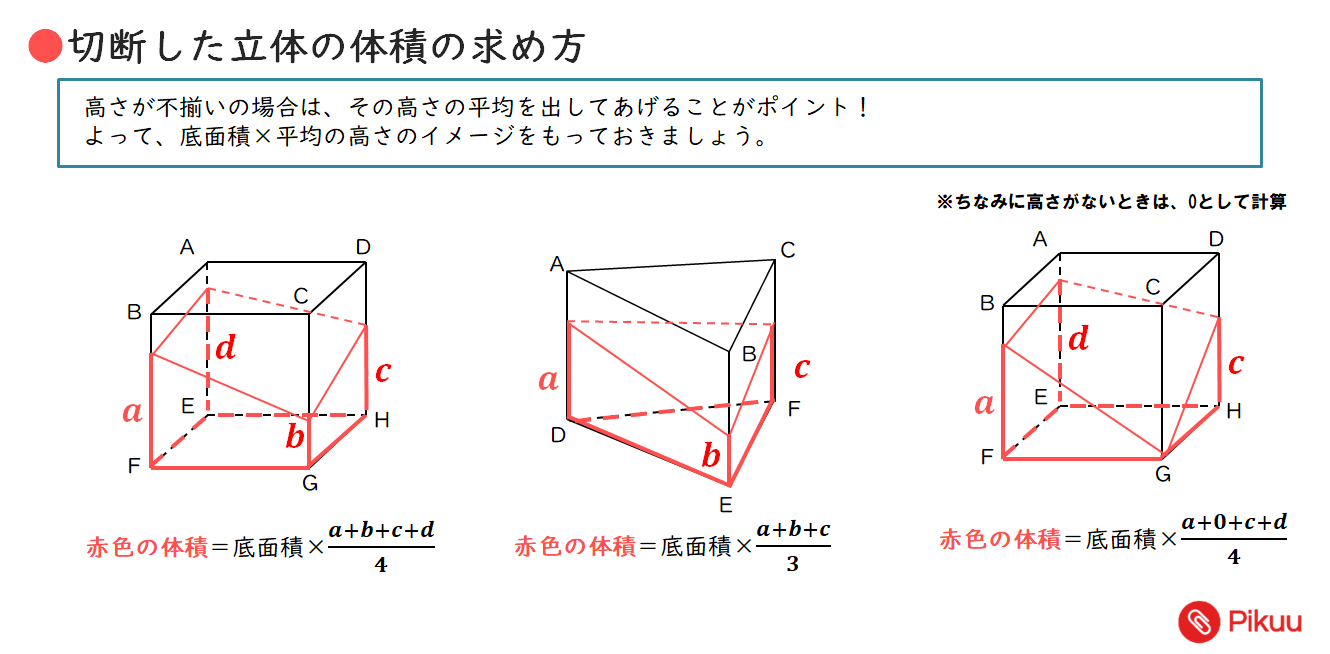


高校入試対策数学 知って得 中学数学の公式テクニック集 Pikuu



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



数 立体の体積と表面積 直前ノート 中学生 数学のノート Clear



数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



側面に接する曲線の長さ Okwave


3分でわかる 円錐の体積 表面積の求め方 合格サプリ



中3 三角形の相似 円錐の体積比 日本語版 Youtube



斜軸回転体の体積 応用編 傘型積分 おいしい数学



数学というより算数です 円錐の側面積について Okwave


子供向けぬりえ 元の三角錐 表面積 求め方 公式


立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学


円錐とは 体積 表面積の公式や求め方 受験辞典



円柱の表面積 あんず学習塾のメモ 図表置き場



中学2年 図形 中学数学に関する質問 勉強質問サイト



角柱の表面積 Youtube


1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
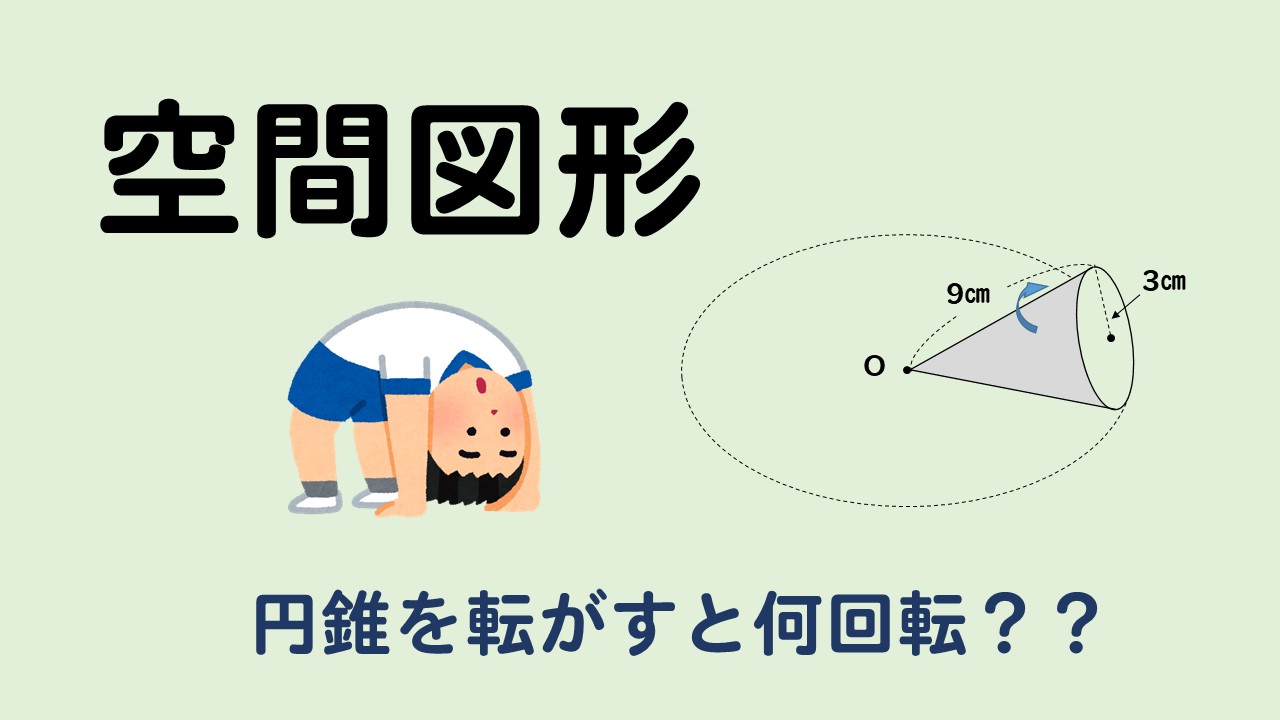


円錐を転がすと1周するのにどれくらい回転する 入試問題を解説 数スタ



円錐の表面積 Youtube



空間図形14 円すい台の体積 Youtube


美しい 正四 角錐 体積 公式 壁紙 配布



円錐の表面積 あんず学習塾のメモ 図表置き場



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方



円錐の表面積の求め方 中学1年数学 Youtube



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル



年の最高 図形 の 面積 無料の印刷物
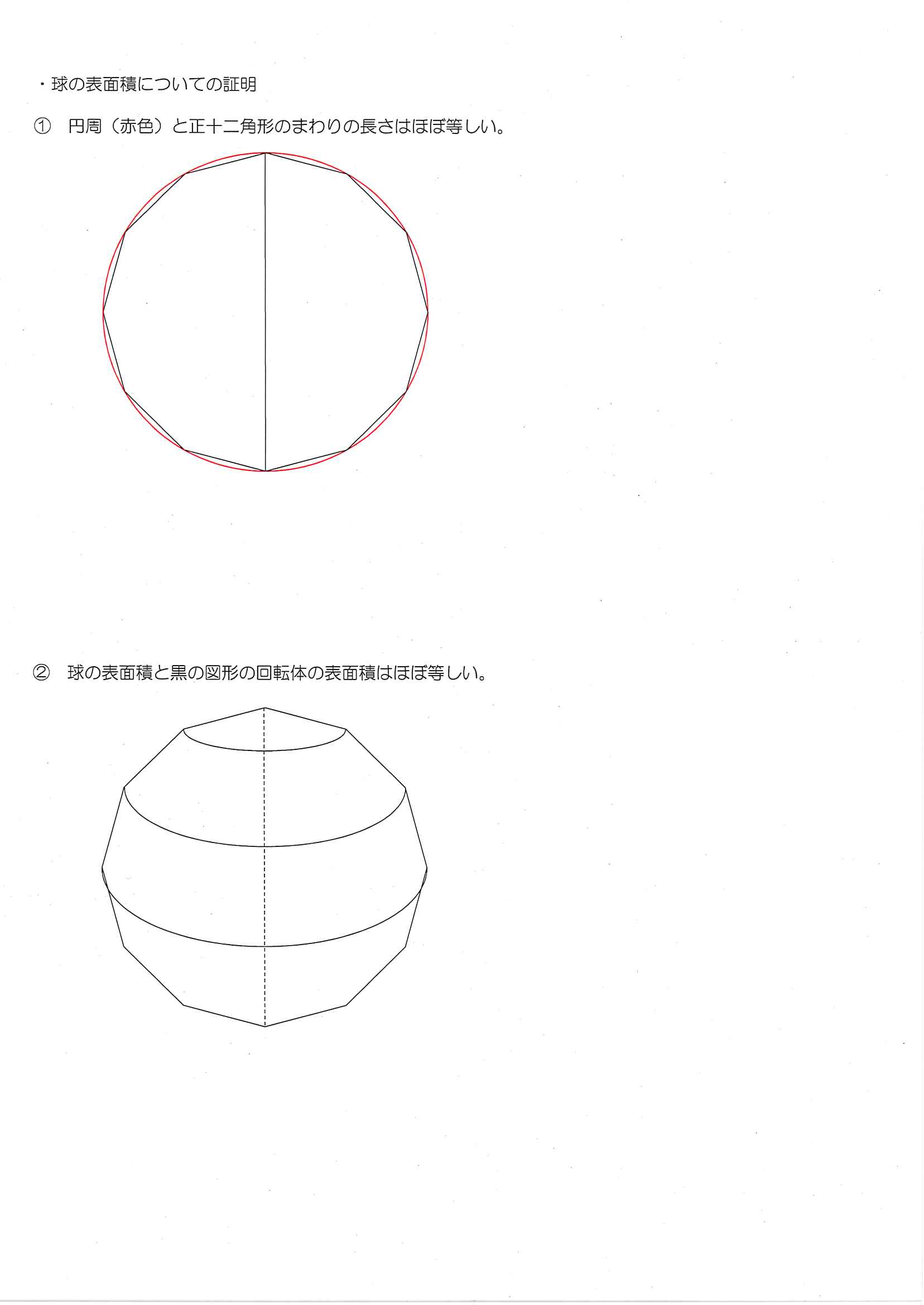


優雅 球体 表面積 求め 方 壁紙 配布



円錐の表面積を 中心角を使って求める チーム エン



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



学校では教えてくれない 円錐表面積簡単公式 中学生 数学のノート Clear


Tossランド 円錐の表面積 Dl可



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



壮大 台形 体積 求め 方 壁紙 配布



中1数学 円すいの問題 練習編 映像授業のtry It トライイット



中1苦手克服シリーズ 回転体 図をイメージしてみよう 中学生 数学のノート Clear
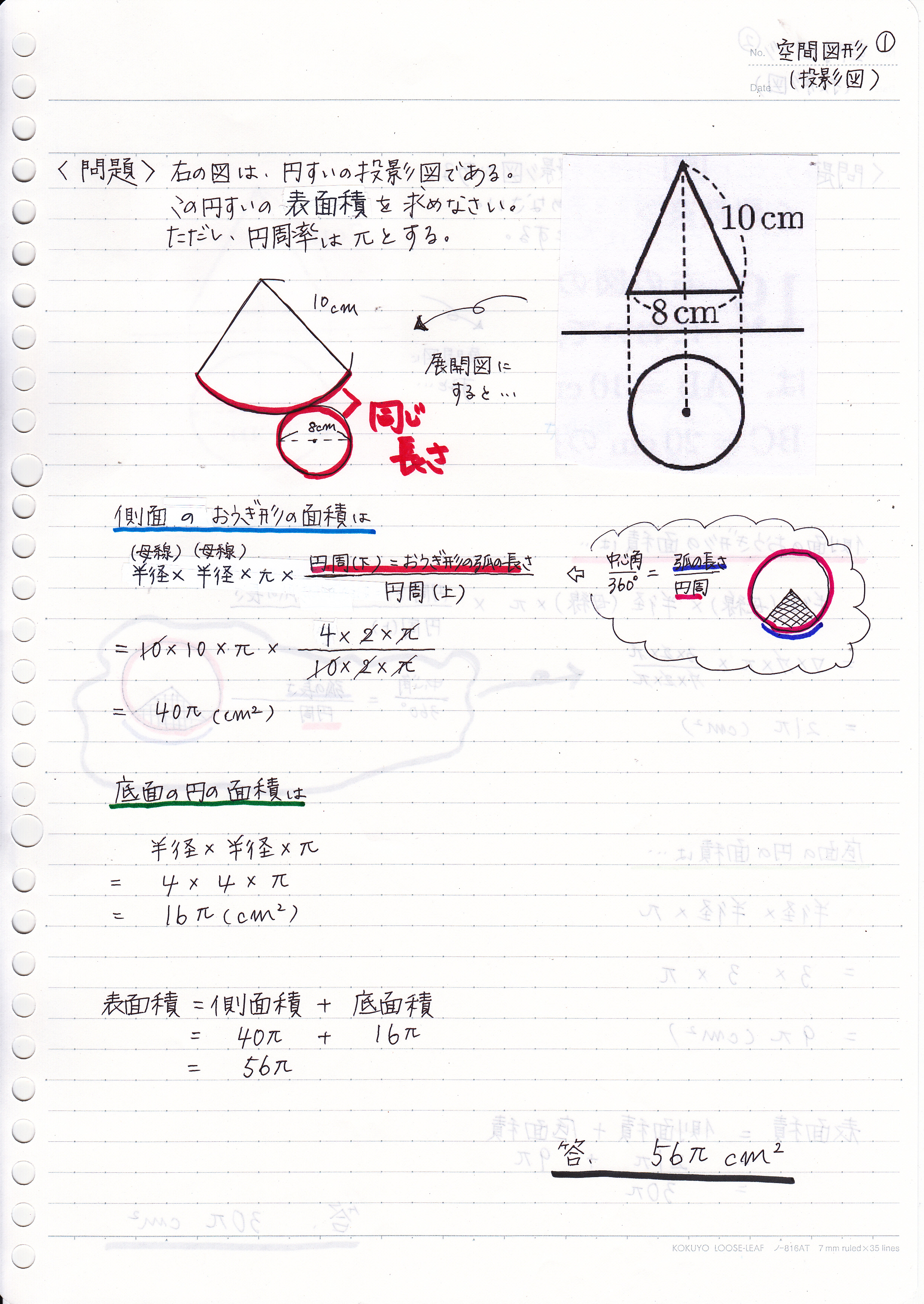


投影図から表面積を求める問題 2問 現役塾講師のわかりやすい中学数学の解き方
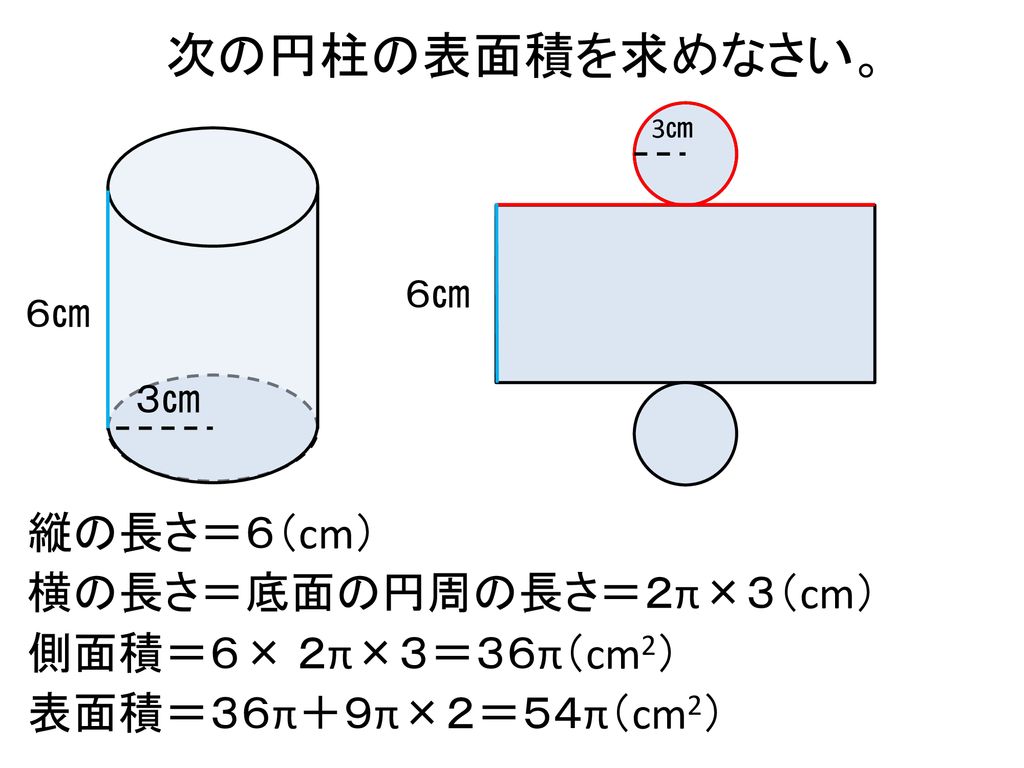


本時の目標 いろいろな立体の表面積を求めることができる Ppt Download



0 件のコメント:
コメントを投稿