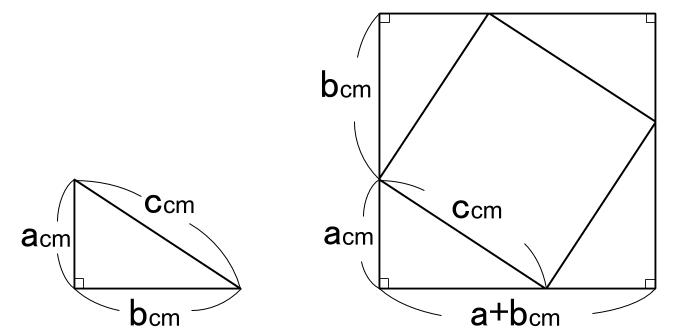
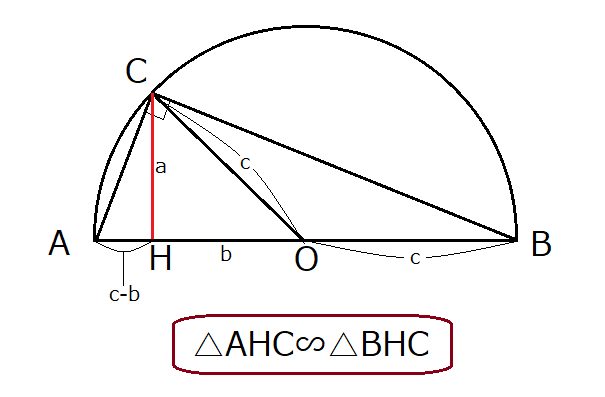
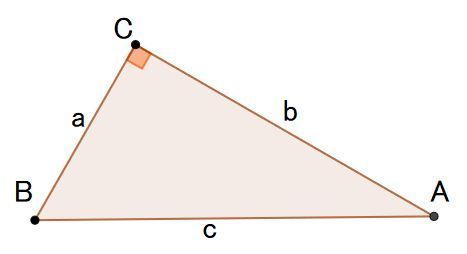
今回は『三平方の定理』という単元を 基礎から解説していきます。 三平方の定理は、いつ習う？ 学校によって多少の違いはありますが 大体は3年生の3学期に学習します。 中3の終盤に学習するにも関わらず 入試にはバンバンと出題されてきます。この記事ではこんなことを書いています 三平方の定理（ピタゴラスの定理）には多くの証明方法がありますが、ここでは円を利用した証明を紹介しましょう。 図形を描いて、その長さを調べていくだけで三平方の定理が証明できてしまう面白い証明方法です。 三平方の定理の簡単な復習 三平三平方の定理 下の図のように直角三角形のそれぞれの辺を 1辺 とする 正 方形P、Q、R の面積にはどんな関係があるかな？ 直角三角形の三辺の長さを a、b、c とすると、 正方形P の
Host 三 平方 の 定理 証明 簡単" /> 三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも
三 平方 の 定理 証明 簡単
三 平方 の 定理 証明 簡単-だから、三平方の定理の逆は 「 c 2 ＝a 2 ＋b 2 が成り立てば 直角三角形 である。 」 だね。 これをを証明しよう！ よって、 ABCと A'B'C'で、三斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理（三平方の定理）の証明は、百以上知られている。
Host 三 平方 の 定理 証明 簡単"> 
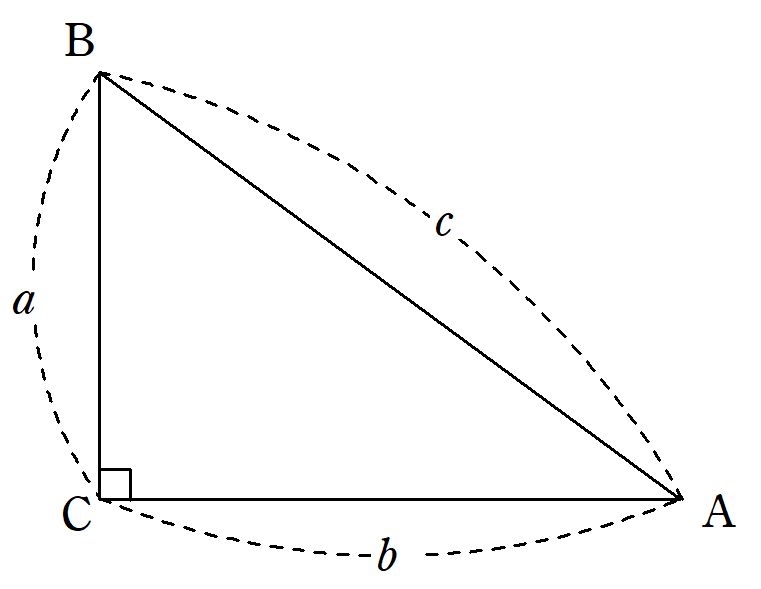
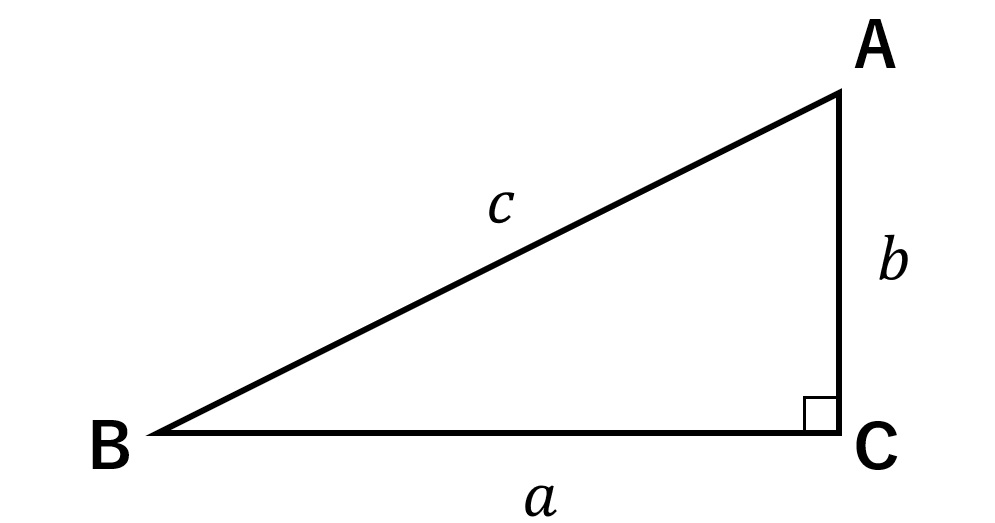
三平方の定理
芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。ピタゴラスの定理の証明と無理量の発見 ･･････ 上垣 渉 「三平方の定理の証明」の授業 数学史のスパイスを効かせて，見方や考え方を広げる ･･････ 荒木 昇;
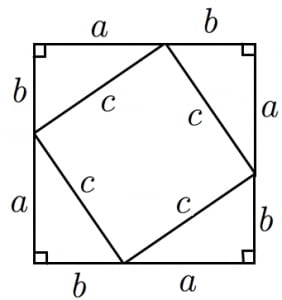
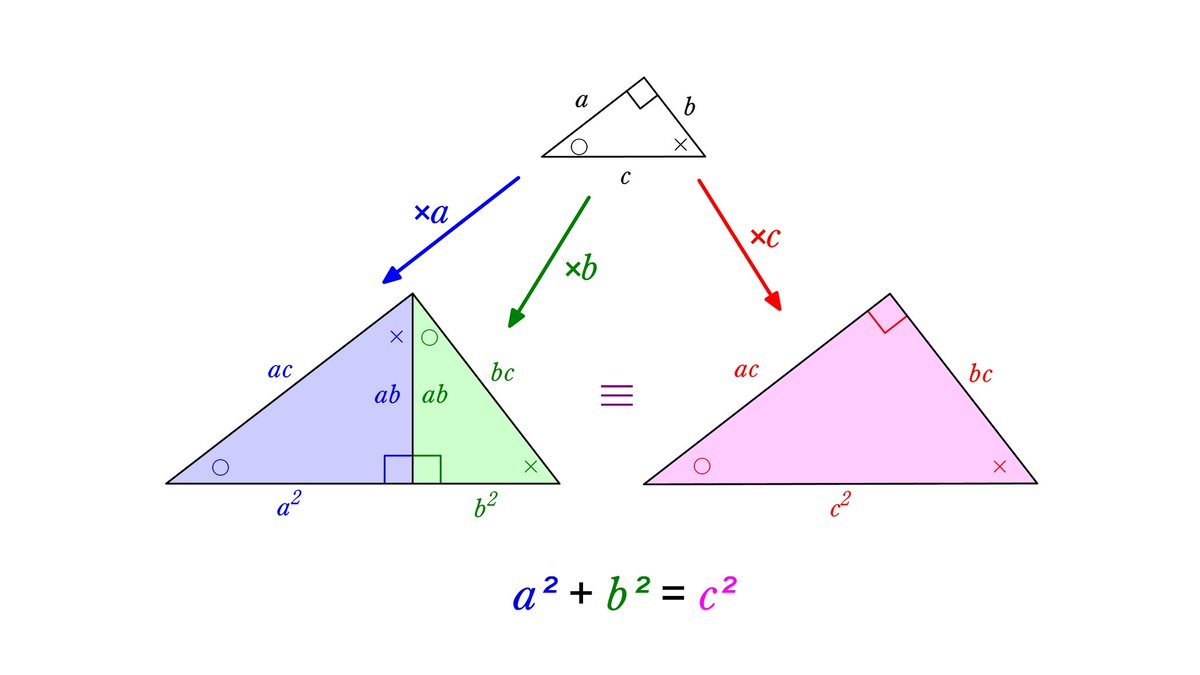
が成り立ちます。これで、三平方の定理を証明することができました！「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。三 平方 の 定理 証明 種類 三平方の定理が、数学が苦手な人でも必ず理解できます。公式の説明だけでなく、三平方の定理の公式の証明、計算方法と解き方、暗記すべき比と角度、計算問題まで紹介しています。この記事だけで三平方の定理について三平方の定理には数百もの証明方法があります。今回は第代アメリカ合衆国大統領のジェームズ・A・ガーフィールドが思いついた証明方法について紹介します。 Ⅰ 三平方の定理とは Ⅱ ジェームズ・A・ガ
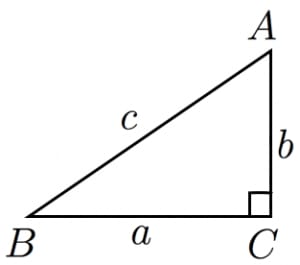
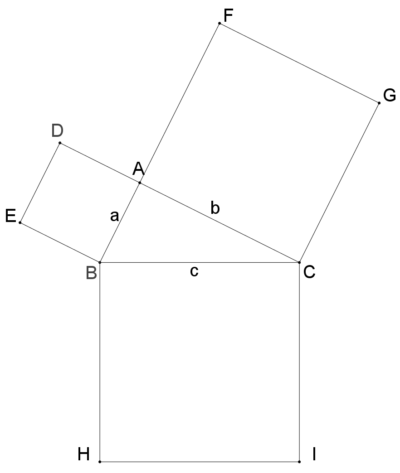
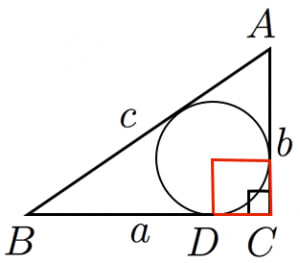
三平方の定理には数百もの証明方法があります。今回は相似を利用した基本的な証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理（ピタゴラスの定理三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べる。 このときa 2 b 2 =c 2 となることを次のように証明した。 空欄ア、イに適切な文字または数字を入れよ。すなわち 点pはabの三等分点です。 正方形を2回折るだけ，意外と簡単に三等分点を見つけることができます。 これも三平方の定理を使って証明できました。
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 正方形の面積を使う方法 数学教材
Host 三 平方 の 定理 証明 簡単"> 証明にこだわる
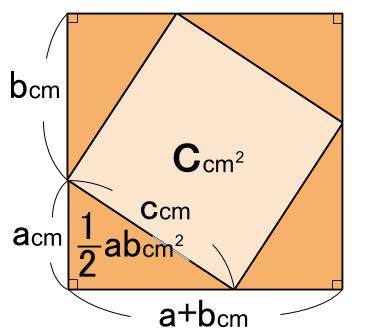
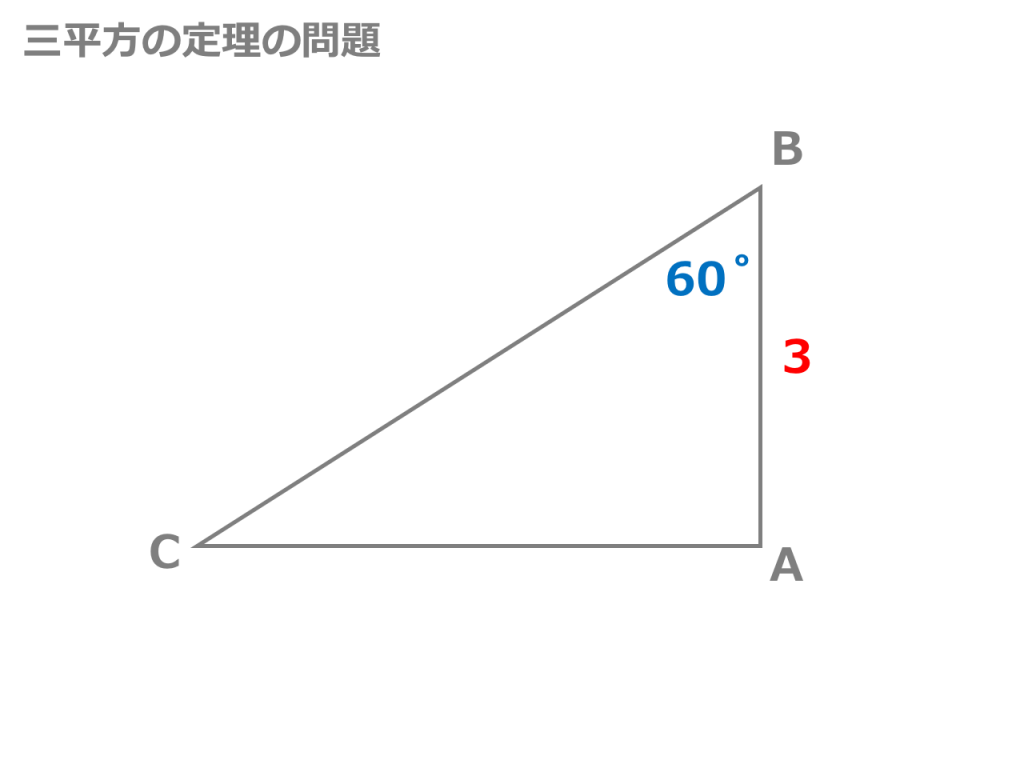
三平方の定理の証明 三平方の定理はなぜ成立するのか。 ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか？ 実に様々な証明がありますが、 中学生が学習しておくべき最も重要な証明を紹介します。 三平方の定理 証明の例 下図のような直角三角形を \(4\) つをスムーズな導入といろいろな証明 ･･････ 木谷 直充三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
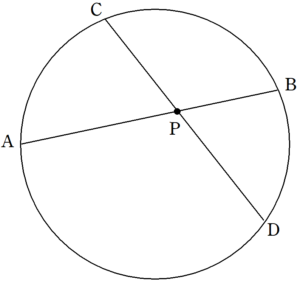
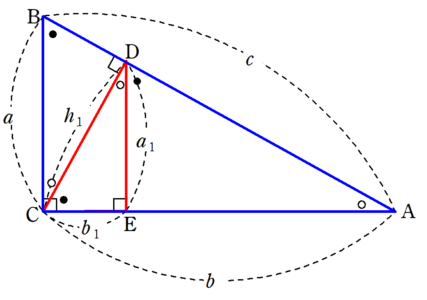
モーリーの定理の証明 §1 はじめに． モーリー（ Edward Williams Morely, ）の定理というのは「任意の三角形の各頂角の三等分線 が各辺により近い三つの交点によって作る小三角形は正三角形である」（ 図2 参照 ）という定理である．中線定理とは 中線定理とは、図の ABCにおいて辺BCの中点をMとするとき、 であるというものでした。 中線定理の証明 これを証明してみましょう。 まず、頂点Aから辺BCに垂線を下ろし、その交点をHとします。 ABHに三平方の定理をあては斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理（三平方の定理）の証明は、百以上知られている。
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の４通りの美しい証明 高校数学の美しい物語
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 方べきの定理の利用１ Fukusukeの数学めも
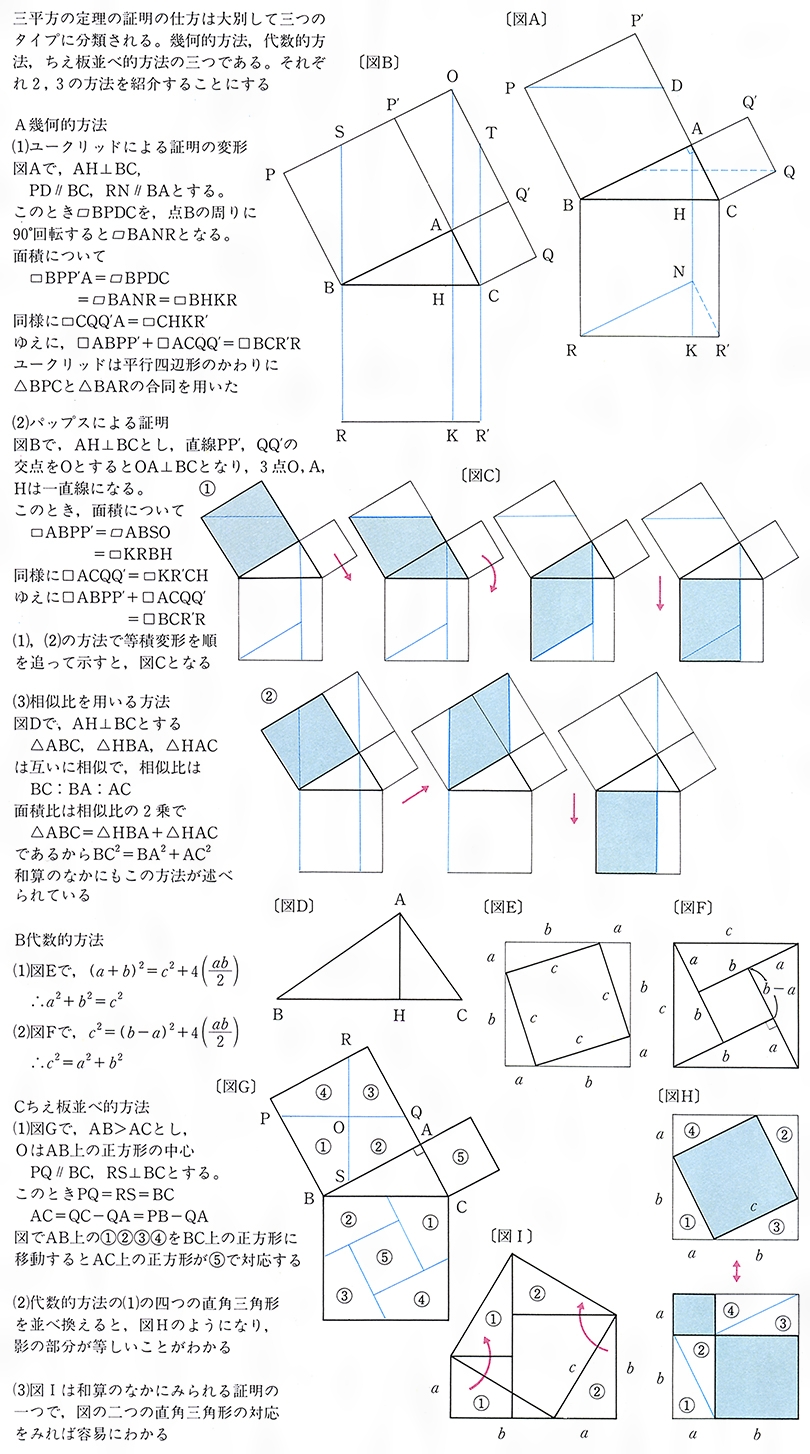
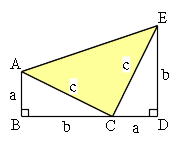
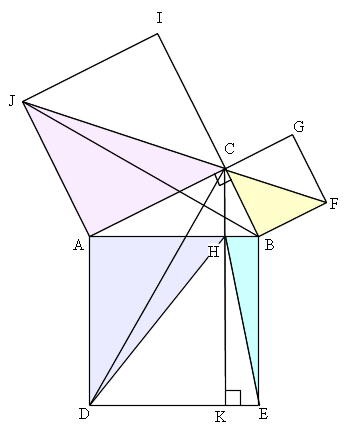
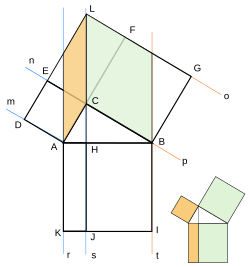
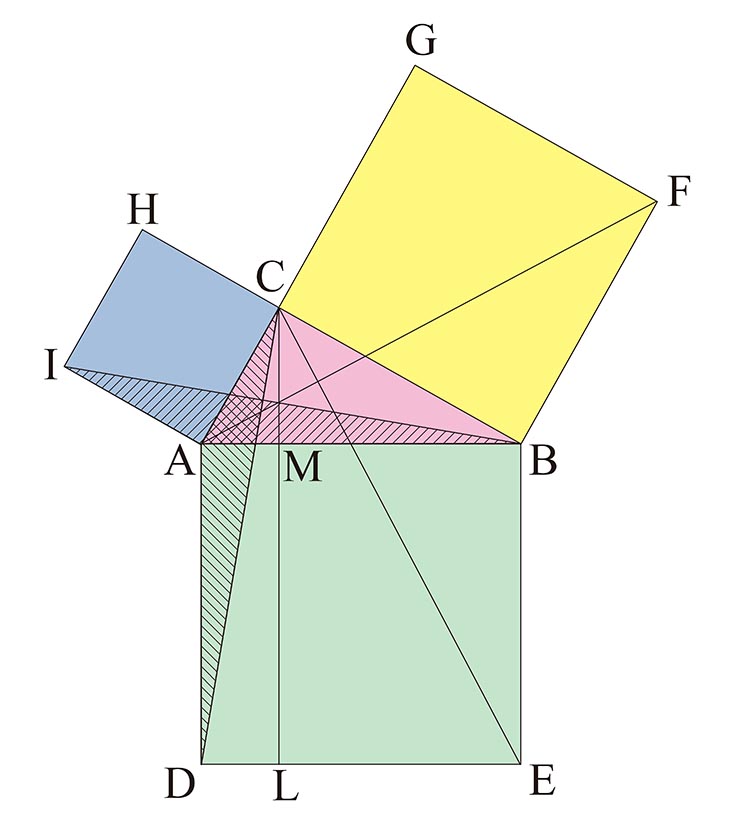
ありません。三平方の定理の逆の証明として，間接証明法である同一法がありますが，直接証明法ではない証明 法があることを知る機会として，証明の全体の流れを理解できる程度に扱うとよいでしょう。 三平方の定理の逆の証明について 中学数学 3年3－1②三平方の定理 証明パズル 1 H I 2 A c G B F C ピタゴラスの肖像 D E 正方形bdecの 対角線の交点 を通り，辺ab と辺biに平行 な直線をひく 三平方の定理 証明パズル 2 H I 2 A c G B F C D E 頂点dを通って 辺abに平行な 直線をひく。 その直線と辺 ceとの交点かこの記事ではこんなことを書いています 三平方の定理（ピタゴラスの定理）には多くの証明方法がありますが、ここでは円を利用した証明を紹介しましょう。 図形を描いて、その長さを調べていくだけで三平方の定理が証明できてしまう面白い証明方法です。 三平方の定理の簡単な復習 三平
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の逆の証明
モーリーの定理の証明 §1 はじめに． モーリー（ Edward Williams Morely, ）の定理というのは「任意の三角形の各頂角の三等分線 が各辺により近い三つの交点によって作る小三角形は正三角形である」（ 図2 参照 ）という定理である．
Host 三 平方 の 定理 証明 簡単"> 三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 Wikipedia
Host 三 平方 の 定理 証明 簡単"> トップ 100 三 平方 の 定理 証明 簡単 壁紙 配布
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の４通りの美しい証明 高校数学の美しい物語
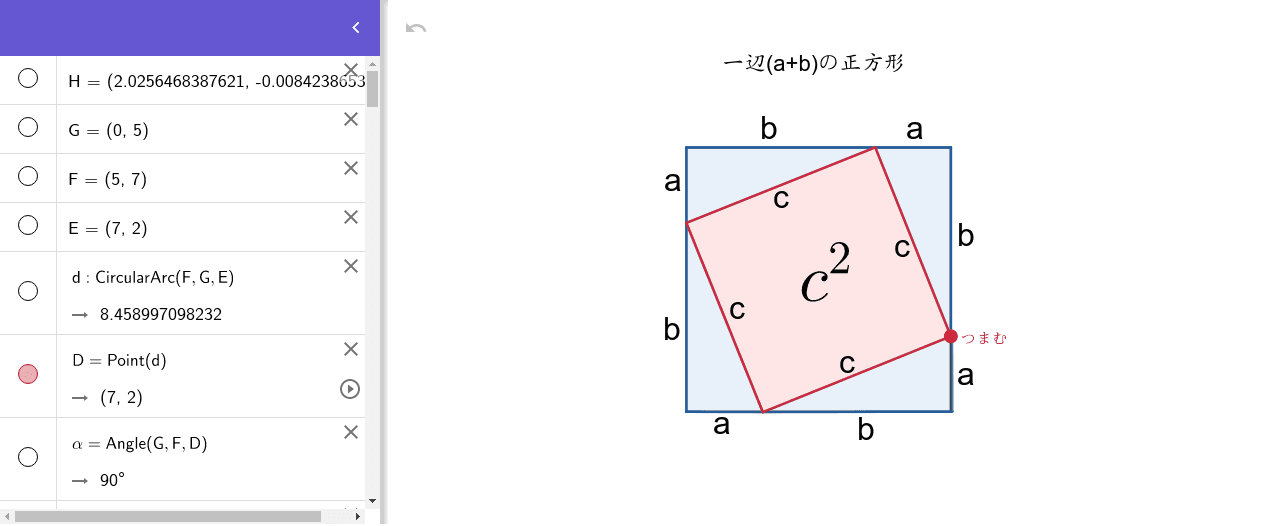
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 証明 Geogebra
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> ポテト一郎 三平方の定理 一番好きな証明です
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明と使い方
Host 三 平方 の 定理 証明 簡単"> コラム ピタゴラスの定理 江戸の数学
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> Mathematics 三平方の定理 １ 三平方の定理の証明 働きアリ
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 中３数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 ピタゴラスの定理
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 Wikipedia
Host 三 平方 の 定理 証明 簡単"> 三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張
Host 三 平方 の 定理 証明 簡単"> 必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明と使い方
Host 三 平方 の 定理 証明 簡単"> 必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
Host 三 平方 の 定理 証明 簡単"> 中学数学 三平方の定理
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理の証明 大栗博司のブログ
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 Geogebra
Host 三 平方 の 定理 証明 簡単"> 中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
Host 三 平方 の 定理 証明 簡単"> 必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
Host 三 平方 の 定理 証明 簡単"> 高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 直感的に分かる図で解説します 数学fun
Host 三 平方 の 定理 証明 簡単"> Mathematics 三平方の定理 １ 三平方の定理の証明 働きアリ
Host 三 平方 の 定理 証明 簡単"> 三平方の定理について考える１ 教科書 大日本図書 の証明方法 身勝手な主張
Host 三 平方 の 定理 証明 簡単"> 中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
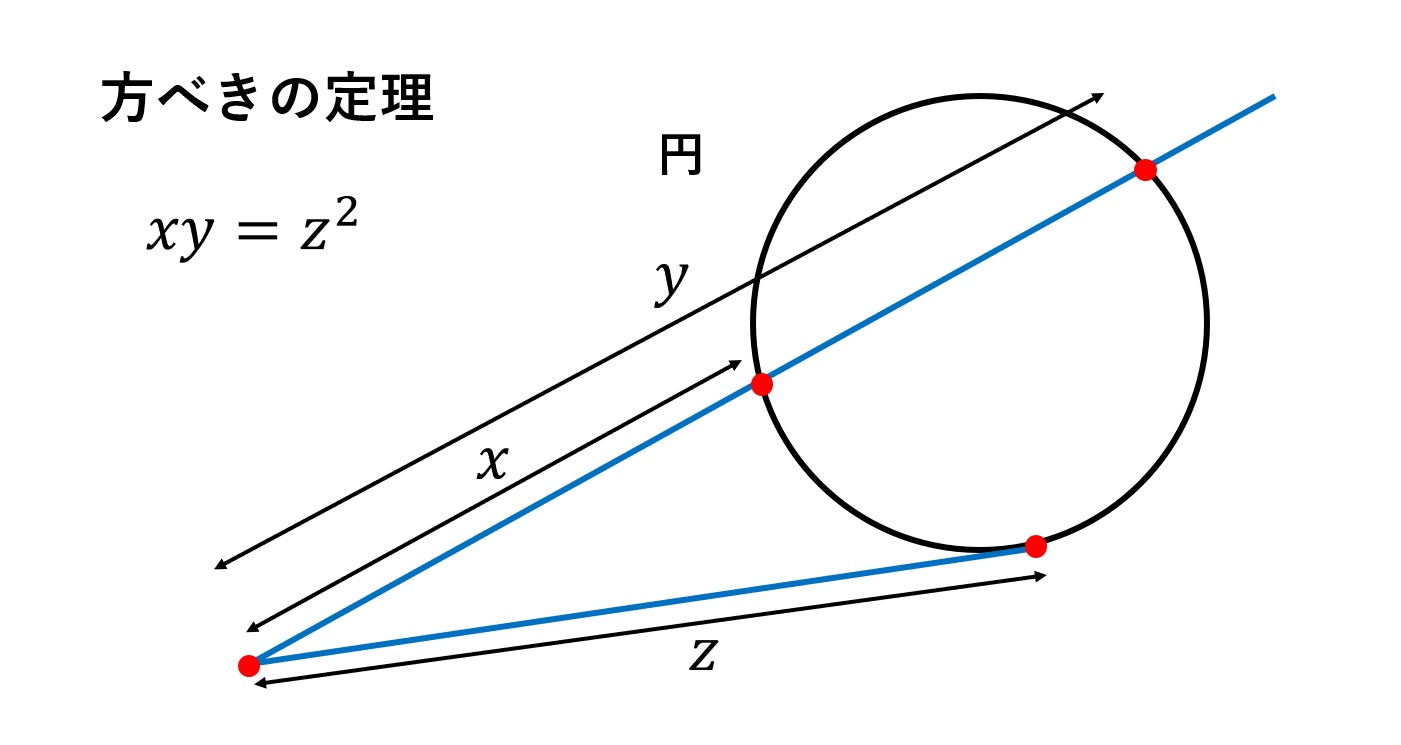
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 方べきの定理の利用１ Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 三石 数学塾 三平方の定理の証明 その２
Host 三 平方 の 定理 証明 簡単"> 数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube
Host 三 平方 の 定理 証明 簡単"> Studydoctor三平方の定理の証明 中学３年数学 Studydoctor
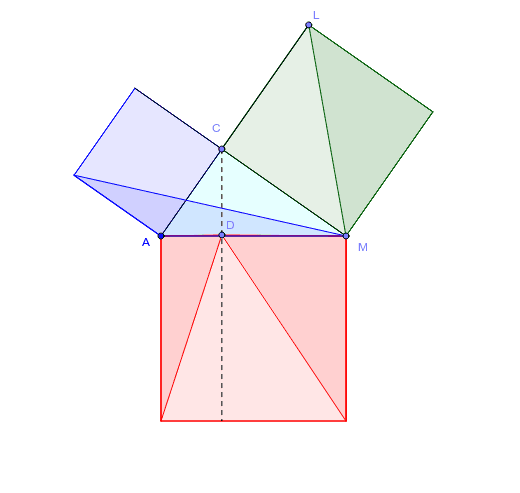Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 ユークリッドの証明 Geogebra
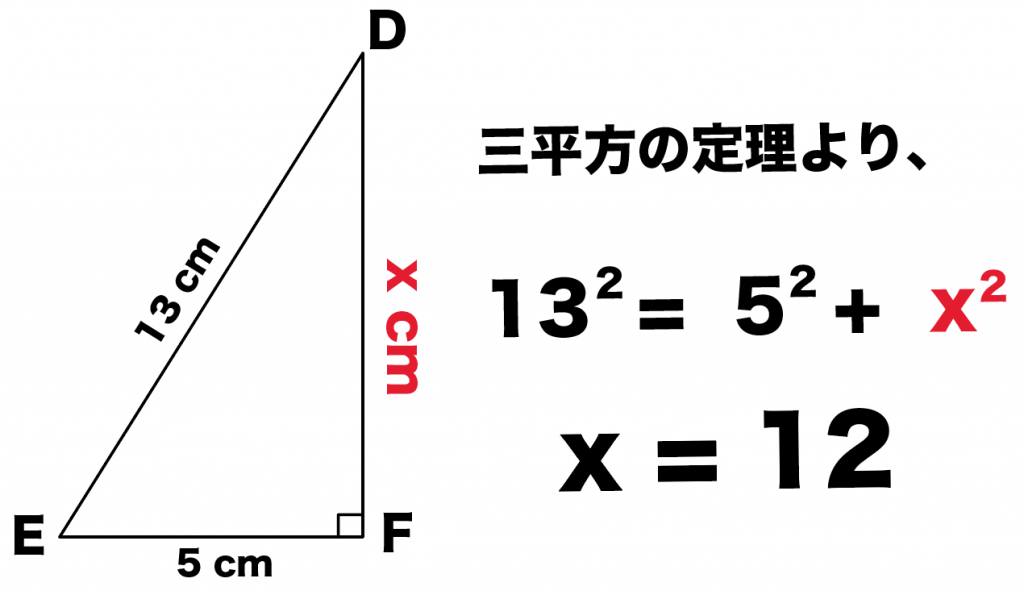Host 三 平方 の 定理 証明 簡単"> 3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 の証明アニメ6 ユークリッド Youtube
Host 三 平方 の 定理 証明 簡単"> 中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 証明の展覧会
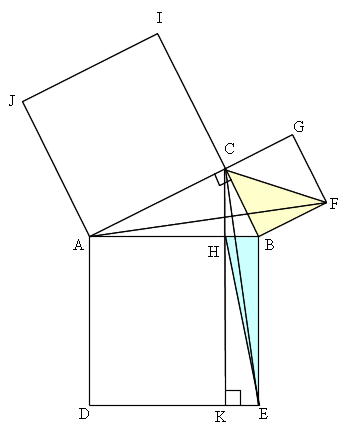Host 三 平方 の 定理 証明 簡単"> Mathematics 三平方の定理 １ 三平方の定理の証明 働きアリ
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 の証明アニメ4 バスカラ Youtube
Host 三 平方 の 定理 証明 簡単"> 必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
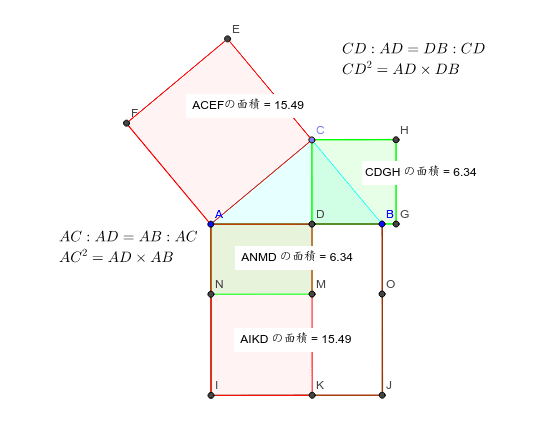Host 三 平方 の 定理 証明 簡単"> 三平方の定理 証明１６ Geogebra
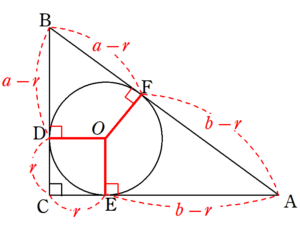
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 内接円の利用 Fukusukeの数学めも
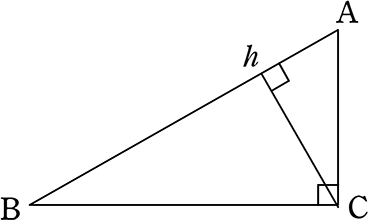
Host 三 平方 の 定理 証明 簡単"> 三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
Host 三 平方 の 定理 証明 簡単"> カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 方べきの定理の利用２ Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の４通りの美しい証明 高校数学の美しい物語
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> 三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
Host 三 平方 の 定理 証明 簡単"> 三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の４通りの美しい証明 高校数学の美しい物語
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 ピタゴラスの定理とはあまり言いたくない キソカラ
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 相似な三角形を使う方法 数学教材
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理とその証明
Host 三 平方 の 定理 証明 簡単"> 必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
Host 三 平方 の 定理 証明 簡単"> 3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
Host 三 平方 の 定理 証明 簡単"> 正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
Host 三 平方 の 定理 証明 簡単"> ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> ピタゴラスの定理 Wikipedia
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> 小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ
三平方の定理の最も変わった証明方法はなんですか Quora
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
Host 三 平方 の 定理 証明 簡単"> 中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明 相似を利用した証明２ Fukusukeの数学めも
Host 三 平方 の 定理 証明 簡単"> 中学数学 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
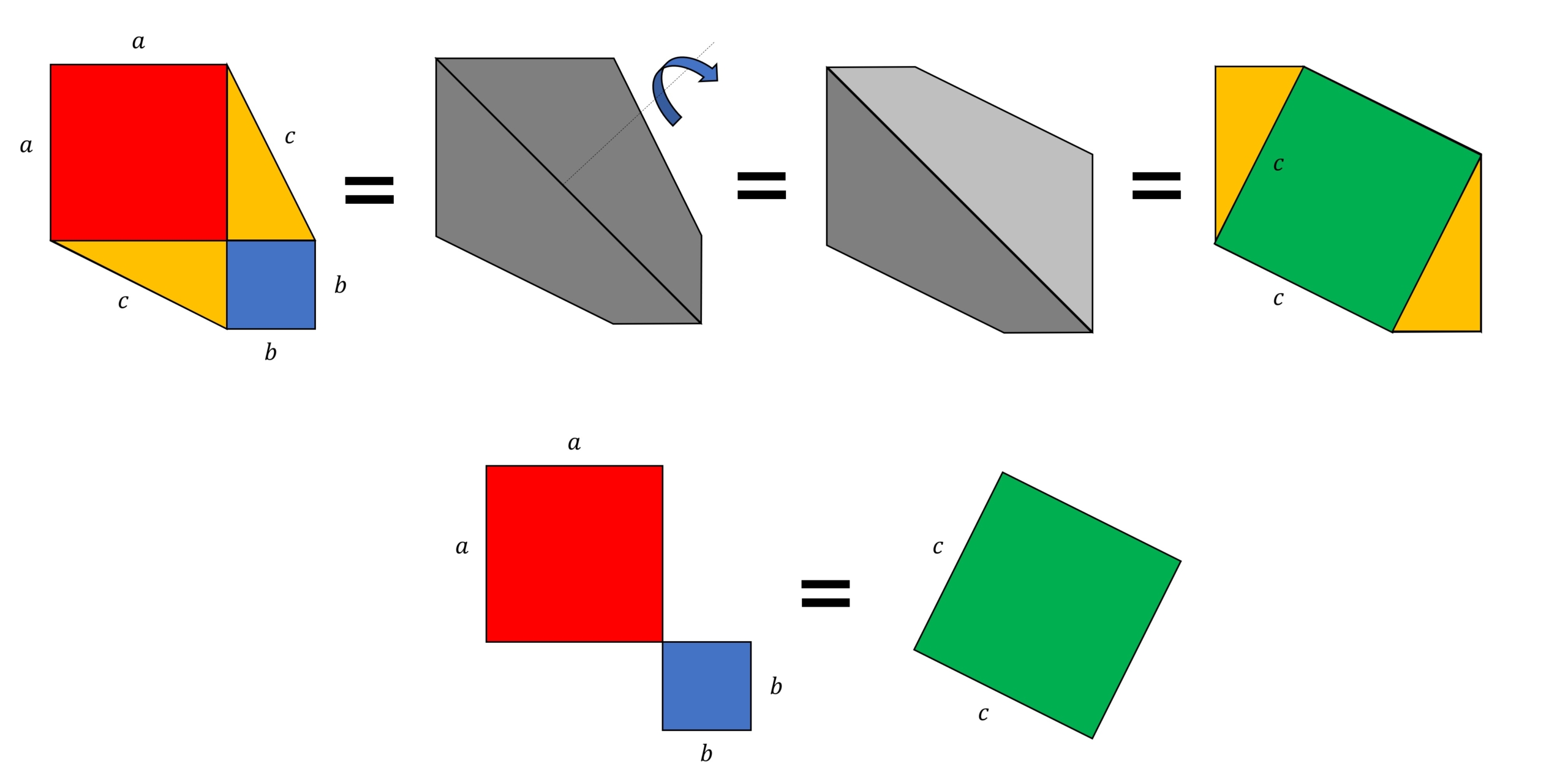
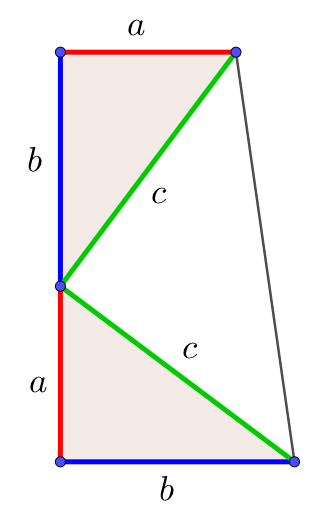
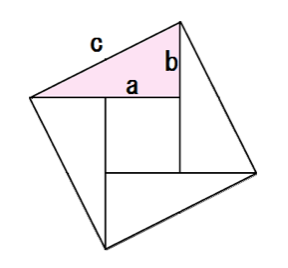
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明３ 大統領の台形 キソカラ
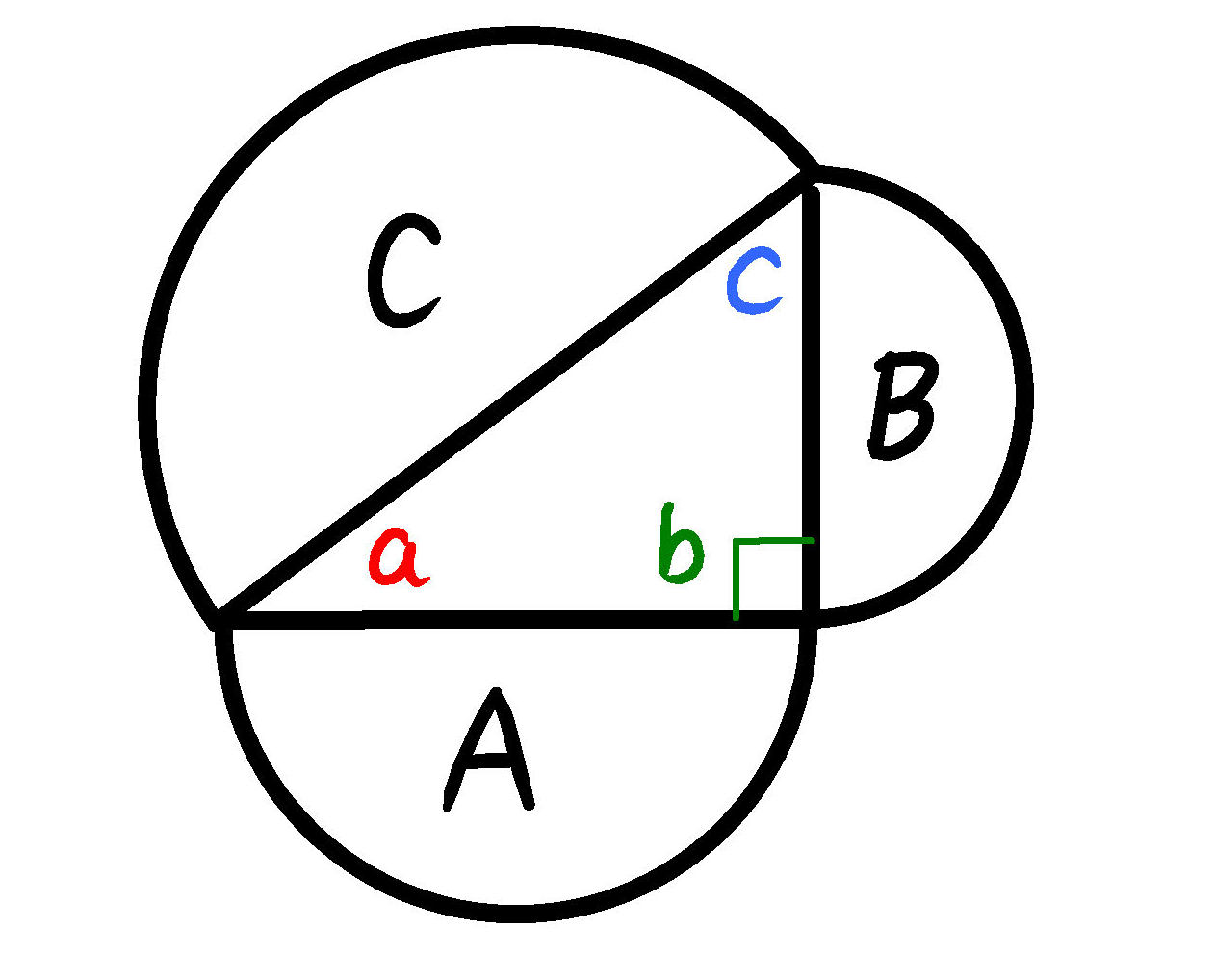
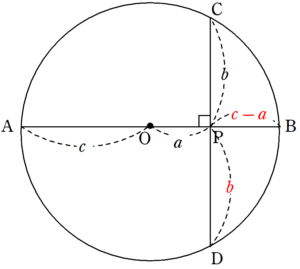
Host 三 平方 の 定理 証明 簡単"> 円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
Host 三 平方 の 定理 証明 簡単"> 三平方の定理とは 証明方法や例題についても解説 スタモ 受験 入試 学習の総合サイト
Host 三 平方 の 定理 証明 簡単"> 三平方の定理の証明２ ４つ直角三角形と真ん中の四角 キソカラ
Host 三 平方 の 定理 証明 簡単"> 中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
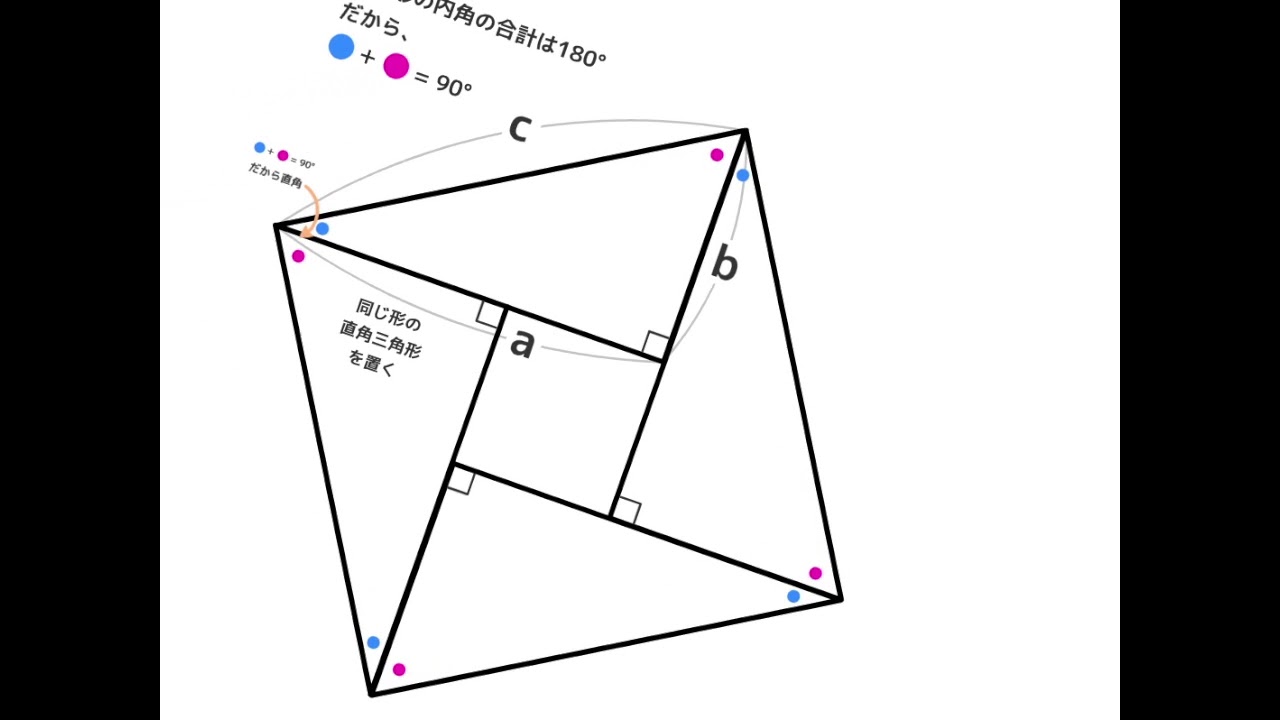
Host 三 平方 の 定理 証明 簡単"> 中3数学 三平方の定理が成り立つ理由を超図解 Youtube
Host 三 平方 の 定理 証明 簡単"> 中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく
Host 三 平方 の 定理 証明 簡単"> 三平方の定理
Host 三 平方 の 定理 証明 簡単"> 三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ
Host 三 平方 の 定理 証明 簡単"> 中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
Host 三 平方 の 定理 証明 簡単"> 三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
Host 三 平方 の 定理 証明 簡単"> コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション
0 件のコメント:
コメントを投稿