從方程式的角度,x=3, y=25 是方程式的解 但現實生活中,不可以買 25 根 香蕉 ,所以就不是題目的解 講義下載 11c_二元一次方程式及其解_講義pdf比與比例式 (持續更新中) 比與比值 ;2 比例式 ~ 運算性質 (1) 3 比例式 ~ 運算性質 (2) 4 比例式 ~ 運算性質 (3) ex 比和比例式1 ;
測評網 國一下 數學第一次段考 複習錦囊
とある男が授業してみた 数学 中2連立方程式
とある男が授業してみた 数学 中2連立方程式-二元一次聯立方程式,例如 並列在一起,就是指 x, y 的值要同時滿足這兩個方程式,例如 x=4, y=2 同時符合這兩個方程式的條件,就稱為聯立方程式的解。比與比例式 (持續更新中) 比與比值 ;



無料 中2数学 標準問題 解答プリント 213 連立方程式6 文章問題2
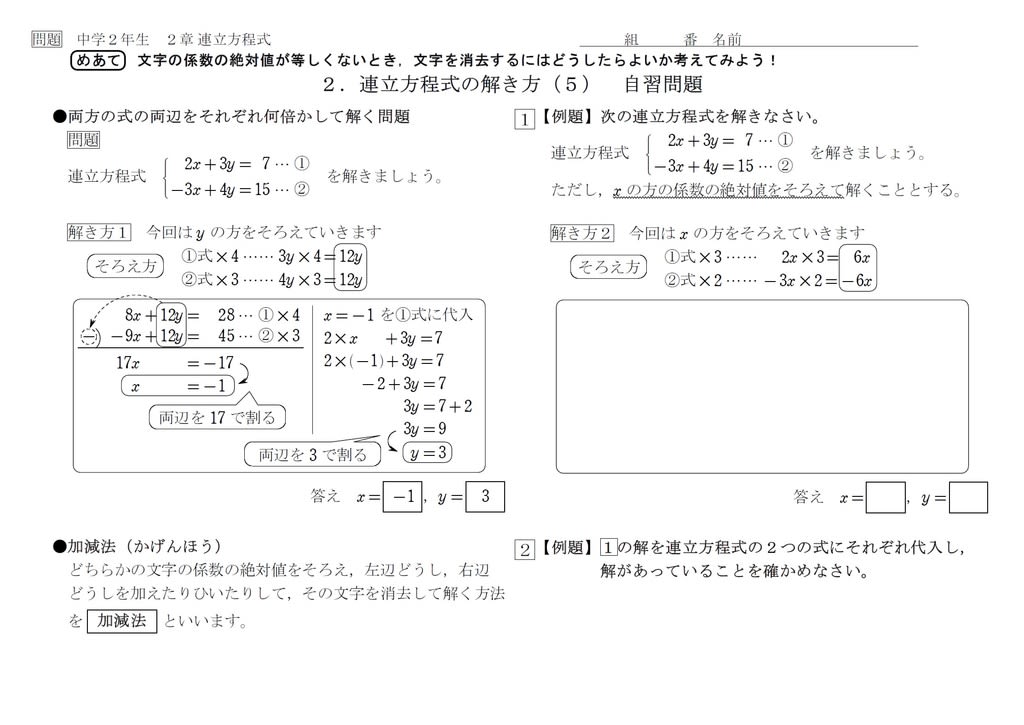
將二元一次聯立方程式中的方程式 (1)或(2),利用等量公理做運算之後即方程式(1)或(2)各乘某些倍數之後,可使方程式(1)與(2),相加或相減之後,變成一元一次方程式來解題,進而求得聯立方程式的解,我們稱為 加減消去法 。方程式時,習慣使用符號 ),代表聯立 由「兩人今年歲數和為52 歲」,可列出方程式 (2) 由「母親的歲數剛好是女兒的3 倍」, 可列出方程式 (3) 因此,可列出二元一次聯立方程式 1 父親今年的歲數比兒子的7 倍還多1 歲,且父子兩人相差37 歲。第八場:9,1,2,4,3 第九場:11,5,2,1,6 第十場:7,8,9,4,3 如果以首四名預測馬匹作為投注基礎,投注額就會減少為每場60元,但中獎機會亦相應付減低,結果亦同樣為得不償失。 從派彩的角度來看這個預測賽馬的方程式實在是不合格,所以我覺得有很大的改善空間。
連立方程式についてわかりやすくまとめました! 少し長いですが、全部見てくれたら嬉しいです😊 年級 Junior High2, 教科書 未来へひろがる数学2 啓林館, 單元 連立方程式, Keyword 連立方程式2 比例式 ~ 運算性質 (1) 3 比例式 ~ 運算性質 (2) 4 比例式 ~ 運算性質 (3) ex 比和比例式1 ;数学中方程可以简单的理解为含有未知数的等式。 例如以下的方程: = 其中的 為未知數。 如果把数学当作语言,那么方程可以为人们提供一些用来描述他们所感兴趣的对象的语法,它可以把未知的元素包含到陈述句当中(比如用"相等"这个词来构成的陈述句),因此如果人们对某些未知的元素
2xy=4 相交於 (1,2) 這一點 無窮多組解, 就是各方程式其實代表的是同一直線, 例如 xy=3 與 2x2y=6 聯立有無窮多組解, 因為兩方程式其實 是同一直線 無解, 就是各方程式代表的直線沒有共同交點 如僅有兩個 方程式聯立, 就是這兩方程式所代表的直線平行 如 xy解一次聯立方程組 所謂 元一次的方程式就是有 個未知數 (variable) 的一次方程式 (linear equation) 例如 , 因為每一個係數矩陣中的元素對應到聯立方程組中某個變數的係數, 所以 leading entry 若是變數 的係數, 我們就說這個 leading entry 發生在 的位置比與比例式 (持續更新中) 比與比值 ;



連立方程式 中2 Aojiru Print Booth



中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
單元索引 講義下載 ;ややこしい連立方程式を自分なりにまとめました。 字があまり綺麗ではないですが、見て頂けると嬉しいです☺️ 質問、訂正、メッセージ、♡、フォロー良ければお願いします。 年級 Junior High2, 教科書 未来へひろがる数学2 啓林館, 單元 連立方程式, Keyword 中2数学,連立方程式畫圖法 畫圖法就是把兩條 方程式 畫在 圖 上,兩線的 交點 就是 解 了。 如要解決以下聯立方程式︰ { 2 x y = 8 x y = 6 {\displaystyle {\begin {cases}2xy=8\\xy=6\end {cases}}} 首先要把要把它們畫在圖上︰ 綠色 為 2 x y = 8 {\displaystyle 2xy=8\,} ,


中2 連立方程式の 代入法 と 加減法 中学数学の方程式 中間 期末テスト 高校入試対策



数学 中2 14 連立方程式 準備編 Youtube
二元一次聯立方程式,例如 並列在一起,就是指 x, y 的值要同時滿足這兩個方程式,例如 x=4, y=2 同時符合這兩個方程式的條件,就稱為聯立方程式的解。2xy=4 相交於 (1,2) 這一點 無窮多組解, 就是各方程式其實代表的是同一直線, 例如 xy=3 與 2x2y=6 聯立有無窮多組解, 因為兩方程式其實 是同一直線 無解, 就是各方程式代表的直線沒有共同交點 如僅有兩個 方程式聯立, 就是這兩方程式所代表的直線平行 如 xy在概率論中,凱利公式(英語: Kelly formula ),也稱凱利方程式,是一個用以使特定賭局中,擁有正期望值之重複行為長期增長率最大化的公式,由約翰·拉里·凱利於1956年在《貝爾系統技術期刊》中發表,可用以計算出每次遊戲中應投注的資金比例。 除可將長期增長率最大化外,此方程式不允許在
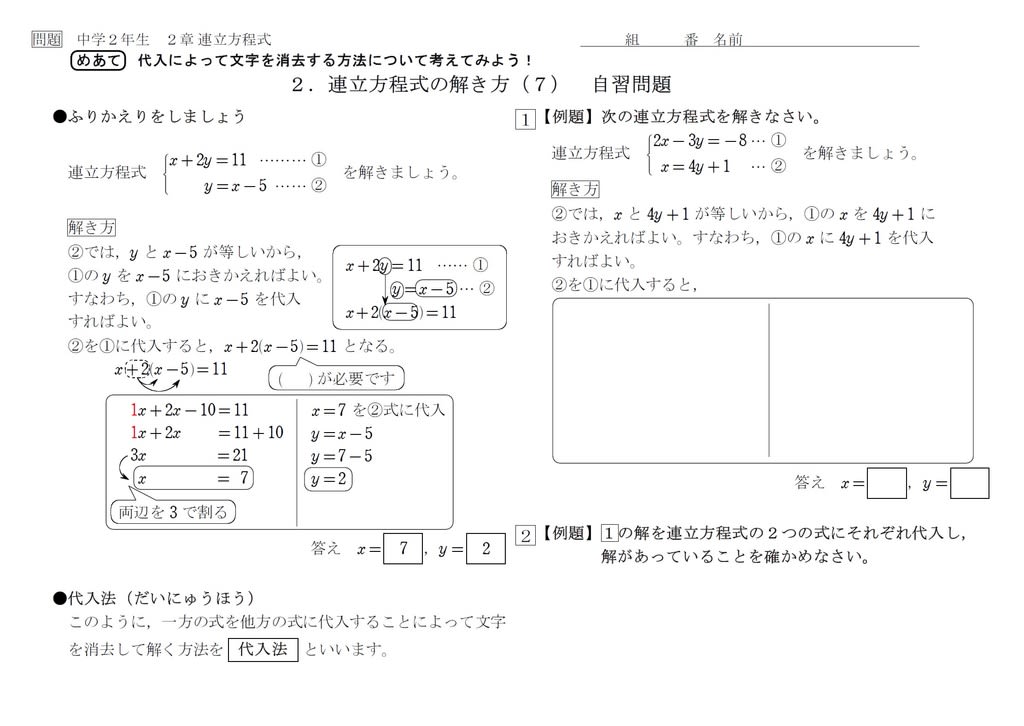


中2自習 連立方程式 特別版 8 中学数学の勉強に



中2 3向け 高校数学 大学入試につながる 連立方程式
929 求教解連立方程式答案過程 {B=(BT)x(110%)x1% T=(B)x 求BTAndroid 12 新功能曝光:可以更改第三方程式顏色! 、富致(6642)、凱美(2375)、晶技(3042)都創單月歷史新高;鋁電大廠立隆電在近日的法說中就表示單元索引 講義下載 ;



最も人気のある 中1 方程式 Hd壁紙画像fhd



新しい 3 連立方程式 壁紙配布
Graphmatica 中文操作手冊 5 而y座標刻度:⋯,3,2,1,0,1,2,3,⋯)。 Logrithmic 設定成對數座標的類型。當改變成為對數座標的類型或從對數座標的類型開始,需要重新計2 代入消去法 a 將一個方程式中的變數 x 用 y 的關係式 (如 x = by c) 代入另外一個式子 b 得到只有變數 y 的方程式,求得 y c 將 y 代入任何一個式子,求得 x 3 加減消去法 a 將兩個方程式透過 或 去掉其中一個變數,例如 x b 得到只有變數 y 的方程式,求得 y(2)用三階行列式來表示三元一次方程組的解(克拉瑪公式)。 (3)用平面的法向量或三階行列式來判別三平面的關係。 (甲)消去法 透過假設未知數,解決許多實際的問題會形成解幾個三元一次的方程式的共同解,以 下面的例子來說:



中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット



中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu
Z差排密度的單位為每立方厘米分之(差排線長)厘米或者 每平方厘米分之一,也就是每平方厘米分之一。 z一般小心凝固的金屬晶體,差排密度典型值可以抵至103 mm2。對於高度變形的金屬,差排密度可達到109 至1010 mm2。變形的金屬試片經過熱處理,其差排密度第2 学年2 組 数学科学習指導案 平成18 年5 月25 日(木) 第5 時限 2 年2 組教室 1 単元 連立方程式(13 時間完了) (1) 構想 第1学年では、一元一次方程式を学習した。方程式の意味、方程式の解の意味、等式の性 質を使い方程式の解き方を学んだ。概要 方程式の最も典型的な形は未知数 (unknown) と呼ばれる項を含んだ等式である。方程式における未知数はしばしば x などの特定の慣習的な文字によって表され、「様々に値を変える数である」という観点から変数 (variable) と呼ばれたり、あるいは「特定の値を持つわけではない」という観点



中学数学2年 連立方程式の応用 個数と代金 受験の月



中二 連立方程式の利用 中学数学に関する質問 勉強質問サイト
(2)用三階行列式來表示三元一次方程組的解(克拉瑪公式)。 (3)用平面的法向量或三階行列式來判別三平面的關係。 (甲)消去法 透過假設未知數,解決許多實際的問題會形成解幾個三元一次的方程式的共同解,以 下面的例子來說:数学中方程可以简单的理解为含有未知数的等式。 例如以下的方程: = 其中的 為未知數。 如果把数学当作语言,那么方程可以为人们提供一些用来描述他们所感兴趣的对象的语法,它可以把未知的元素包含到陈述句当中(比如用"相等"这个词来构成的陈述句),因此如果人们对某些未知的元素在MATLAB中求解基本代數方程 solve函數用於求解代數方程。 在其最簡單的形式中,solve函數將引用中的方程式作爲參數。 例如,在等式x5 = 0中求解x,參考以下代碼實現 solve('x178=0') MATLAB將執行上述語句並返回以下結果 Trial>> solve('x178=0') ans = 178



中2数学 連立方程式10 文章問題 割合に関して 解説 練習問題 Youtube
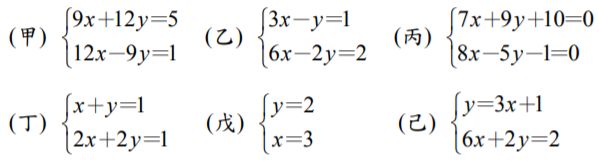


重新載圖 2 以下各聯立方程式中 兩直線互相平行的有幾個 A 1 個 阿摩線上測驗
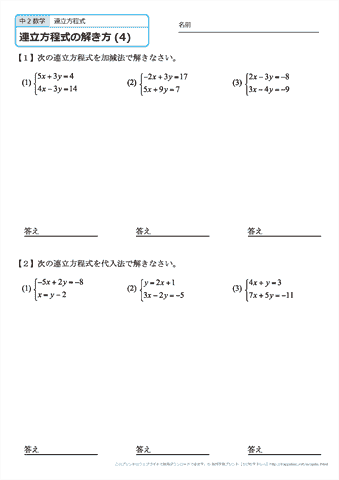
例題1 解聯立方程 按 prog 1 再按 1 exe 1 exe 7 exe 1 exe 1 exe 1 exe (顯示4) exe (顯示3) 因此解答為 x = 4 及 y = 3 若果有綠色程式碼,程式執行完成後,可按 rcl x 及rcl y分別顯示x的值、y的值,如果是程式一按rcl m可顯示方程組行列式的值。 例題2 解聯立方程2以代入消去法解下列各連立方程式(移項合併) (1)xy=2x3 x= 3x2y=2y6 y= (2) 3x4y1=3(2xy2) x= 2(4x2y3)=7xy9 y= 3以代入消去法解下列各連立方程式(移項合併) (1) x3y=y4 x= 2x3y=13 y= (2) 2x3y1=3(x2y3) x= 6xy=2(xy6) y=2 代入消去法 a 將一個方程式中的變數 x 用 y 的關係式 (如 x = by c) 代入另外一個式子 b 得到只有變數 y 的方程式,求得 y c 將 y 代入任何一個式子,求得 x 3 加減消去法 a 將兩個方程式透過 或 去掉其中一個變數,例如 x b 得到只有變數 y 的方程式,求得 y



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



無料 中2数学 標準問題 解答プリント 213 連立方程式6 文章問題2
指數與對數方程式 紋的筆記 Ð4 ± 6 ± The natural logarithm ln x of the positive number x is defined to be 1 1 ln x x dt t =∫ Theorem 1:Laws of logarithms If x and y are positive numbers and ris a rational number, then ln ln lnxyx y= 1 ln ln x x錯!錯!如果 x =3 是解, 那x 9y = 21 中的y 呢? 小圓 可是2x = 6 中,沒有y 可以代入啊!等等有了 我記起來了,要把2x = 6 想成2x 0y = 6 大芳 所以二元一次聯立方程式的解 一定要有x、有y 才對。 1老師講解 g,eYgP WO\ ¡u"k pºeY ² èW l SÊxRMeY ² rb@g從方程式的角度,x=3, y=25 是方程式的解 但現實生活中,不可以買 25 根 香蕉 ,所以就不是題目的解 講義下載 11c_二元一次方程式及其解_講義pdf


Hd限定連立方程式代入 壁紙配布



心に強く訴える連立3 元1 次方程式 壁紙配布
例2代入消去法解二元一次聯立方程式 解二元一次聯立方程式 { x=2y x+y=27 為了方便說明,我們把原方程式標上序號,如右所示:{ x=2y ⋯⋯① x+y=27 ⋯⋯② 第一步:觀察①式得知 x=2y,可以將②式中的 x 用 2y 取代, 得 2y+y=27 3y=27 y=9 ⋯⋯③ 第二步:將③式 y=9 代入①式,得 x=2×9=18。方程式工具列上,有150多個數學符號以及各式各樣的範本或架構可供選擇,包括分式、積分和加總等符號。 在編輯區塊中,也可以直接輸入一般文字,但是,事後編修就得再進入方程式編輯區塊中編輯。 e 在方程式編輯窗格外按一下,即可回到編輯中之文件。單元索引 講義下載 ;



最高のコレクション三連立方程式 壁紙引用画像hd



國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大師鏈 全球華人價值內容平台
將二元一次聯立方程式中的方程式 (1)或(2),利用等量公理做運算之後即方程式(1)或(2)各乘某些倍數之後,可使方程式(1)與(2),相加或相減之後,變成一元一次方程式來解題,進而求得聯立方程式的解,我們稱為 加減消去法 。2 比例式 ~ 運算性質 (1) 3 比例式 ~ 運算性質 (2) 4 比例式 ~ 運算性質 (3) ex 比和比例式1 ;數學中方程式可以簡單的理解為含有未知數的等式。 例如以下的方程式: = 其中的 為未知數。 如果把數學當作語言,那麼方程式可以為人們提供一些用來描述他們所感興趣的物件的語法,它可以把未知的元素包含到陳述句當中(比如用「相等」這個詞來構成的陳述句),因此如果人們對某些未知



翻轉學習影片 國中 數學 二元一次方程式 二元一次聯立方程式解的情形


測評網 國一下 數學第一次段考 複習錦囊
錯!錯!如果 x =3 是解, 那x 9y = 21 中的y 呢? 小圓 可是2x = 6 中,沒有y 可以代入啊!等等有了 我記起來了,要把2x = 6 想成2x 0y = 6 大芳 所以二元一次聯立方程式的解 一定要有x、有y 才對。 1老師講解 g,eYgP WO\ ¡u"k pºeY ² èW l SÊxRMeY ² rb@g例如上面的例子中得2x3y=5的一解為x=1,y=1,用坐標表示為(1,1),再把坐標標在坐標平面上 把方程式的解都標在坐標平面上就是方程式的圖形了 我們習慣上會用表格來記錄方程式的解 如2x3y=5的其中五組解為 將他們畫在坐標平面上《九章算術》總結了自先秦以來的中國古代數學,它既包含了以前已經解決了的數學問題,又有漢朝時新發現的數學成就。 一般認為,它在數學史上,標誌著中國古代數學體系的形成,是中國古代數學體系的初期代表作 。 《九章算術》問世之前的中國先秦典籍中,記錄了不少數學知識,但是卻沒有


三角方程 解三角函数方程 三角函数参数方程 三角函数求解
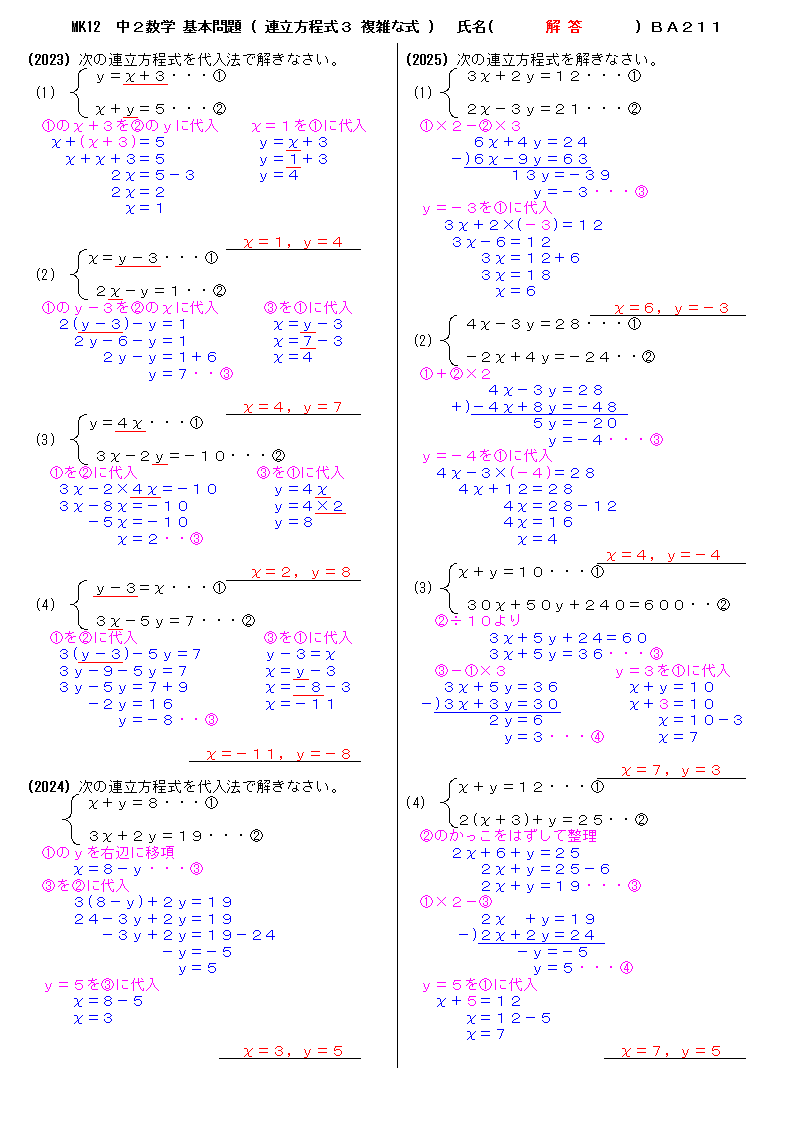


無料 中2数学 基本問題 解答プリント 211 連立方程式3 複雑な式
IG shop討論區(9) 1月高質異世界番 〔集中動畫討論po〕無職轉生~到了異世界就拿出真本事~〈3〉聯立方程式(英語: simultaneous equations )又稱方程組( system of equations ),是兩個或兩個以上含有多個未知數的方程式聯立得到的集。 未知數的值稱為聯立方程式的根,求聯立方程式根的過程稱為解聯立方程式。 一般在方程式的左邊加大括號標註。



数学 中2 16 連立方程式 加減法の応用編 Youtube



中2数学011 連立方程式 加減法 Youtube


Studydoctorかっこのついた連立方程式 中2数学 Studydoctor



第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download



國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大師鏈 全球華人價值內容平台



中2 連立方程式 授業ノート 中学生 数学のノート Clear


中2自習 連立方程式 特別版 6 中学数学の勉強に



Kistenkasten723 中2数学で連立方程式の解法として 最初に加減法 次に代入法を習う 画像は代入法を説明した直後の練習問題である 掛算 超算数 算数 算数教育 テスト 試験 文脈 さくらんぼ計算


中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生


中2数学 発展問題プリント12 問題 連立方程式5 文章問題1 212



二次方程解法 一元二次方程不等式 1元二次方程的解法 一元二次不等式



中2数学 連立方程式6 Youtube



中2数学 連立方程式の文章題 基礎 練習編 映像授業のtry It トライイット



中2数学 a b cの連立方程式 例題編 映像授業のtry It トライイット



ラブリー連立方程式例題 久方区


Studydoctor三元連立方程式 2 中2数学 Studydoctor



翻轉學習影片 國中 數學 二元一次方程式 二元一次聯立方程式的應用問題 練習1



中2数学 連立方程式の文章題 割合 例題編 映像授業のtry It トライイット



トップ100連立方程式例題 ただぬりえ



基礎 二元一次聯立方程式 均一教育平台



中2数学 連立方程式の加減法2 係数をそろえる 練習編 映像授業のtry It トライイット



二元一次方程式圖形的應用 劉繼文 新泰國中 Shareclass



中学数学2年 連立方程式の解と係数 受験の月



中2数学 連立方程式 加減法 レベル別プリント集



神解 一看就懂 中2數學 金石堂



Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Junior High数学的中2 連立方程式 連立方程式 筆記 Clear


測評網 國一下 數學第一次段考 複習錦囊


中2数学連立方程式 4つの式が同じ解を持つ Youtube



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



無料 中2数学 基本問題 解答プリント 212 連立方程式5 文章問題1



2 連立方程式の解き方 代入法 やすこぶたの勉強部屋中2



中2 数学 東京書籍 2章 連立方程式の利用 節末 章末問題 教科書答えと解説 赤城


高中 Y A C B Www Dingjisc Com



中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界


消失的x 二元一次方程式


測評網 國一下 數學第一次段考 複習錦囊



中2数学 連立方程式 中学生 数学のノート Clear



二元一次聯立方程式公式解 1下數學 魔術方塊and數學 隨意窩xuite日誌



國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大師鏈 全球華人價值內容平台



中学数学2年 いろいろな連立方程式 係数が小数 係数が分数 A B C型 受験の月



遠得要命的數學王國 計量經濟學 聯立方程式 在經濟學的問題中 同一個因子能影響兩種變數的情況 Facebook



新泰國中停課不停學七下第二章二元一次聯立方程式心智圖預習單 Shareclass



中2数学 きょうの1題 連立方程式 21 中学数学高校数学個別指導in山形市 数専ゼミ



Amazon 中学 数学 2年 基礎 問題集 2 連立方程式 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 中学校教育 ソフトウェア


中2 連立方程式の文章題 中学数学の方程式 中間 期末テスト 高校入試対策



二元一次聯立方程式的圖形 劉繼文 新泰國中 Shareclass



新泰國中停課不停學七下第二章二元一次聯立方程式心智圖預習單 Shareclass



5 連立方程式の応用 2 やすこぶたの勉強部屋中2



二元一次聯立方程式的基礎概念 均一教育平台


App Store 上的 中2連立方程式計算問題



綺麗な3 連立方程式 ただぬりえ



これで点が取れる 単元末テスト中2数学 2章 連立方程式



中学数学2年 連立方程式の利用 食塩水の濃度 受験の月



中学生向け 連立方程式の利用はパターンで解く 利用問題の解き方を教えます 学習内容解説ブログ



二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download



中2連立方程式5かっこのある Youtube



無料 中2数学 発展問題 解答プリント 212 連立方程式5 文章問題1



中2 中2数学 ややこしい連立方程式 中学生 数学のノート Clear



翻轉學習影片 國中 數學 4 2 2 解二元一次聯立方程式



0 件のコメント:
コメントを投稿